统计之 - 协方差_数据分析师

协方差分析是建立在方差分析和回归分析基础之上的一种统计分析方法。方差分析是从质量因子(qualitative)的角度探讨因素的不同水平对实验指标影响的差异。一般说来，质量因子是可以人为控制的。回归分析是从数量因子(quantitative)的角度出发，通过建立回归方程来研究实验指标与一个（或几个）因子之间的数量关系。但大多数情况下，数量因子是不可以人为加以控制的。

定义

在概率论和统计学中，协方差用于衡量两个变量的总体误差，而方差是协方差的一种特殊情况，即当两个变量是相同的情况。在X和Y是独立的情况下，期望值分别为E[X]与E[Y]的两个实数随机变量X与Y之间的协方差定义为：

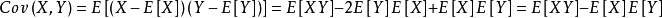
直观上来看，协方差表示的是两个变量总体误差的期望，或者更直白的说协方差用于判定两个变量的相互关联性：

1. 如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值时另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值

2. 如果两个变量的变化趋势相反，即其中一个变量大于自身的期望值时另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值

3. 如果X与Y是统计独立的，那么二者之间的协方差就是0，因为两个独立的随机变量满足E[XY]=E[X]E[Y]。但是，反过来并不成立。即如果X与Y的协方差为0，二者并不一定是统计独立的。

协方差Cov(X,Y)的度量单位是X的协方差乘以Y的协方差。而取决于协方差的相关性，是一个衡量线性独立的无量纲的数。

协方差为0的两个随机变量称为是不相关的。

协方差的属性

两个不同参数之间的方差就是协方差，若两个随机变量X和Y相互独立，则E[(X-E(X))(Y-E(Y))]=0，因而若上述数学期望不为零，则X和Y必不是相互独立的，亦即它们之间存在着一定的关系。

定义

E[(X-E(X))(Y-E(Y))]称为随机变量X和Y的协方差，记作Cov(X，Y)，即Cov(X，Y)=E[(X-E(X))(Y-E(Y))]。

协方差与方差之间有如下关系：

D(X+Y)=D(X)+D(Y)+2Cov(X，Y)

D(X-Y)=D(X)+D(Y)-2Cov(X，Y)

协方差与期望值有如下关系：

Cov(X，Y)=E(XY)-E(X)E(Y)。

协方差的性质：

（1）Cov(X，Y)=Cov(Y，X)；

（2）Cov(aX，bY)=abCov(X，Y)，（a，b是常数）；

（3）Cov(X1+X2，Y)=Cov(X1，Y)+Cov(X2，Y)。

由协方差定义，可以看出Cov(X，X)=D(X)，Cov(Y，Y)=D(Y)。

https://www.cda.cn/

协方差作为描述X和Y相关程度的量，在同一物理量纲之下有一定的作用，但同样的两个量采用不同的量纲使它们的协方差在数值上表现出很大的差异。为此引入如下概念：

定义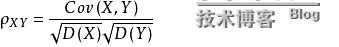称为随机变量X和Y的相关系数。

定义

若ρXY=0，则称X与Y不相关。

即ρXY=0的充分必要条件是Cov(X，Y)=0，亦即不相关和协方差为零是等价的。

定理

设ρXY是随机变量X和Y的相关系数，则有

（1）∣ρXY∣≤1；

（2）∣ρXY∣=1充分必要条件为P{Y=aX+b}=1，（a，b为常数，a≠0）

定义

设X和Y是随机变量，若E(X^k)，k=1，2，...存在，则称它为X的k阶原点矩，简称k阶矩。

若E{[X-E(X)]k}，k=1，2，...存在，则称它为X的k阶中心矩。

若E{(X^k）（Y^p)}，k、l=1，2，...存在，则称它为X和Y的k+p阶混合原点矩。

若E{[X-E(X)]^k[Y-E(Y)]^l}，k、l=1，2，...存在，则称它为X和Y的k+l阶混合中心矩。

显然，X的数学期望E(X)是X的一阶原点矩，方差D(X)是X的二阶中心矩，协方差Cov(X，Y)是X和Y的二阶混合中心矩。

协方差在农业上的应用

农业科学实验中，经常会出现可以控制的质量因子和不可以控制的数量因子同时影响实验结果的情况，这时就需要采用协方差分析的统计处理方法，将质量因子与数量因子(也称协变量)综合起来加以考虑。

比如，要研究3种肥料对苹果产量的实际效应，而各棵苹果树头年的“基础产量”不一致，但对试验结果又有一定的影响。要消除这一因素带来的影响，就需将各棵苹果树第1年年产量这一因素作为协变量进行协方差分析，才能得到正确的实验结果。

当两个变量相关时，用于评估它们因相关而产生的对应变量的影响。

当多个变量独立时，用方差来评估这种影响的差异。

当多个变量相关时，用协方差来评估这种影响的差异。