2018-11-05
阅读量:
1345
简述什么是回归
回归的定义：当存在显着的线性相关时，可以使用线来估计自变量的某些值的因变量的值。
回归方程的适用范围：
- 当存在显着的线性相关性时。也就是说，当你在相关假设检验中拒绝rho = 0的零假设时。
- 在估计中使用的自变量的值接近原始值。也就是说，当x为200时，你不应该使用在10和20之间使用x得到的回归方程来估计y。
- 回归方程不应与不同的人群一起使用。也就是说，如果x是男性的身高，而y是男性的体重，那么你不应该使用回归方程来估计女性的体重。
- 回归方程不应用于预测不是来自该时间范围的值。如果数据来自20世纪60年代，它可能在1990年代无效。
假设你已经确定你可以得到回归方程，因为两个变量之间存在显着的线性相关性，方程式变为：y '= ax + b 或 y '= a + bx （有些书使用y-hat代替Y型素数）。Bluman文本使用第二个公式，然而，更多的人熟悉y = mx + b的概念 ，所以我将使用第一个。
a是回归线的斜率：
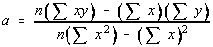
b是回归线的y轴截距：
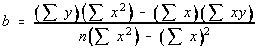
回归线有时被称为“最佳拟合线”或“最佳拟合线”。
回归方程是斜率a穿过该点的线
写这个等式的另一种方法是
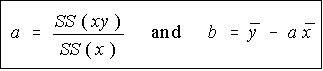
回归线的斜率可以写成
由于标准偏差不能为负，因此斜率的符号由相关系数的符号确定。这与之前的陈述一致，即回归线的斜率与相关系数具有相同的斜率。
0.0000
0
2
关注作者
收藏
评论(0)
发表评论
暂无数据
推荐帖子
CDA持证人阿涛哥
2023-10-12
0条评论
anqiyqi
2023-10-08
0条评论
液冷服务器
2023-09-24
0条评论