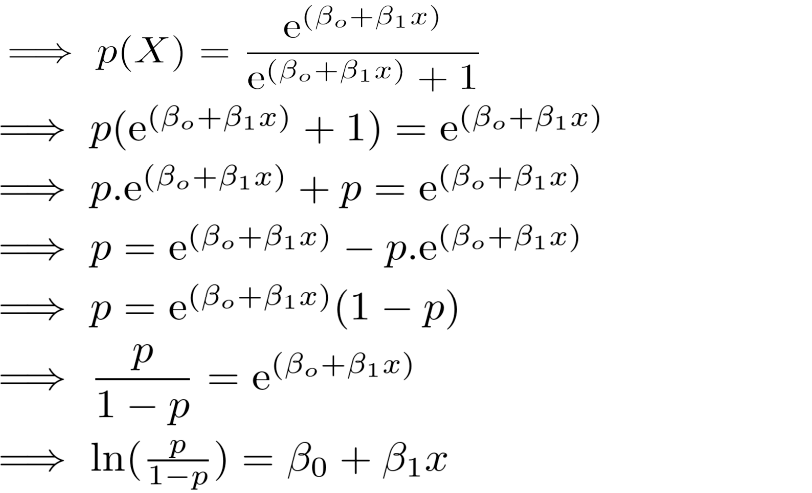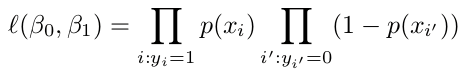众所周知，Logistic回归假设依赖（或响应）变量遵循二项分布。 现在，您可能想知道，什么是二项分布？ 可以通过以下特征来认识下二项分布：

1. 必须有由n表示的固定数量的试验，即在数据集中，必须有固定数量的行。
2. 每次试验只能有两个结果; 即，响应变量只能有两个唯一的类别。
3. 每次试验的结果必须相互独立; 即，响应变量的唯一级别必须彼此独立。
4. 每次试验的成功概率（p）和失败（q）应该相同。

让我们了解Logistic回归的工作原理。 对于线性回归，其中输出是输入要素的线性组合，我们将等式写为：

  `Y = βo + β1X + ∈` 

在Logistic回归中，我们使用相同的等式，但对Y进行了一些修改。 让我们重申一个关于Logistic回归的事实：我们计算概率。并且，概率总是介于0和1之间。换句话说，我们可以说：

1. 响应值必须为正数。
2. 它应该低于1。

首先，我们将满足上述两个标准。 我们知道任何值的指数始终是正数。 并且，任何number除以number + 1将始终低于1.让我们实现这两个发现：

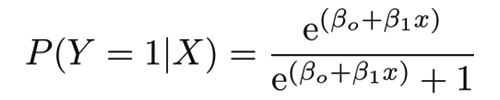
这是逻辑功能。

现在我们确信概率值总是介于0和1之间。要确定链接函数，请仔细遵循代数计算。 P(Y=1|X)可以被解读为“给定x的某个值，Y = 1的概率”。 Y只能取两个值，1或0.为了便于计算，让我们将P(Y=1|X)重写为p(X) 。

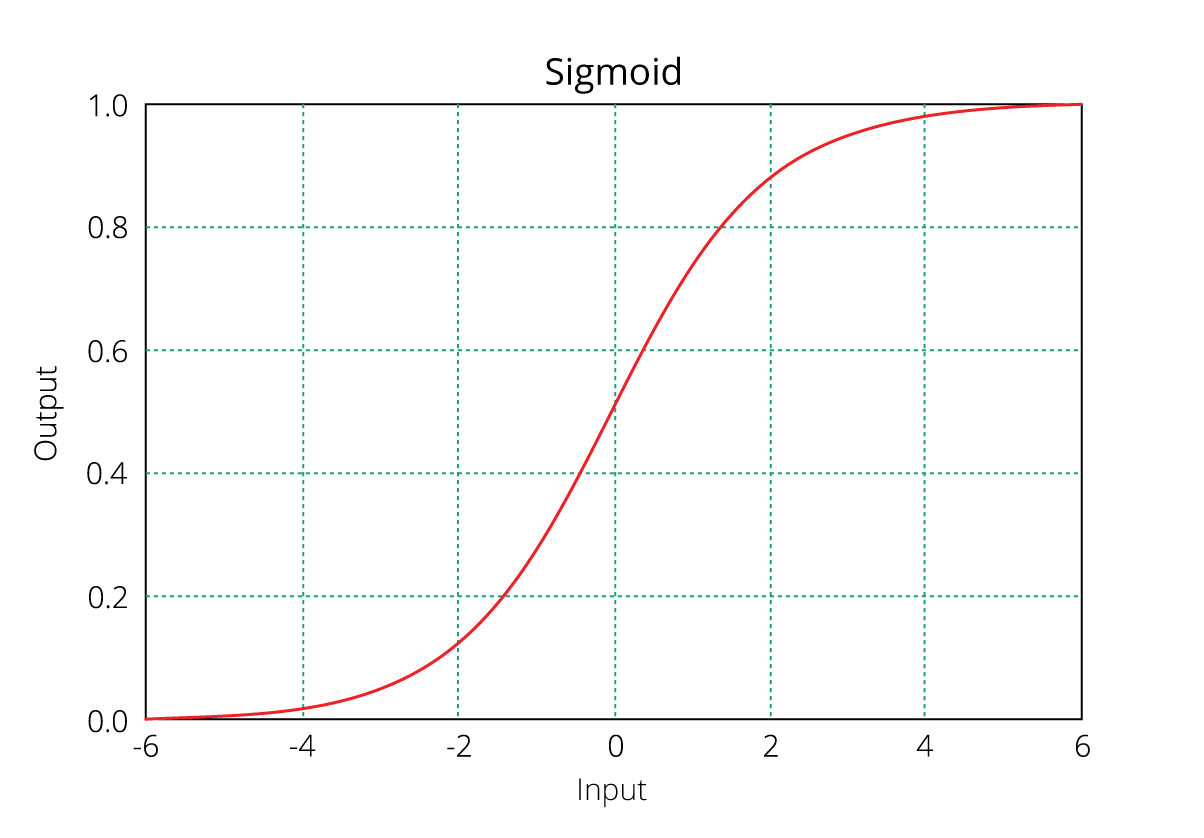
正如您可能认识到的，上面（立即）方程的右侧描述了自变量的线性组合。 左侧称为log - odds或odds ratio或logit函数，是Logistic回归的链接函数。 此链接函数遵循sigmoid（如下所示）函数，该函数将其概率范围限制在0和1之间。

我们可以将上述等式解释为，变量x的单位增加导致比值比乘以ε与幂β 。 换句话说，回归系数解释了预测变量单位变化的响应中log（odds）的变化。 但是，由于p（X）和X之间的关系不是直线，输入特征的单位变化不会直接影响模型输出，但会影响比值比。

这与线性回归相矛盾，其中，无论输入要素的值如何，回归系数始终表示输入要素中每单位增加的模型输出的固定增加/减少。

在多元回归中，我们使用普通最小二乘法（OLS）来确定获得良好模型拟合的最佳系数。 在Logistic回归中，我们使用最大似然法来确定最佳系数并最终确定良好的模型拟合。

最大似然的工作方式如下：它试图找到系数（βo，β1）的值，使得预测概率尽可能接近观察到的概率。 换句话说，对于二元分类（1/0），最大似然将尝试找到βo和β1的值，使得结果概率最接近1或0.似然函数写为