由随机投影p引入的失真由p定义具有良好概率的eps嵌入这一事实来确定：

其中u和v是从形状[n_samples，n_features]的数据集中获取的任何行，而p是具有形状[n_components，n_features]（或稀疏Achlioptas矩阵）的随机高斯N（0,1）矩阵的投影。

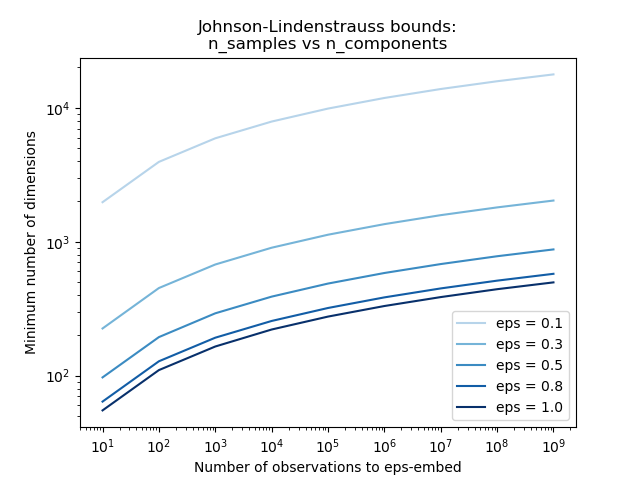
第一个图表显示，随着样本n_samples数量的n_components增加，最小数量的维度以对数方式增加，以保证eps嵌入。

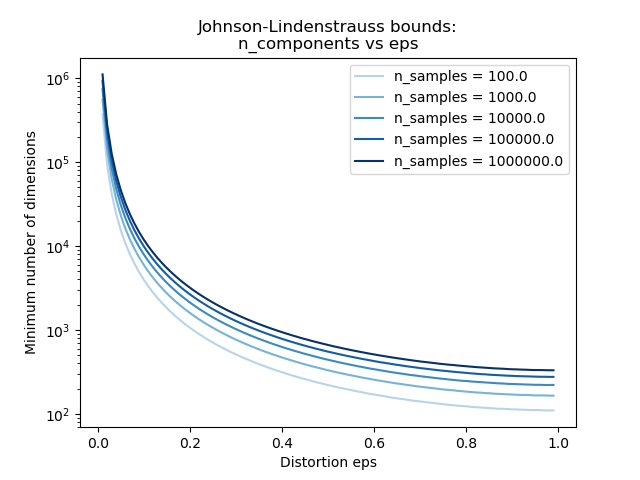
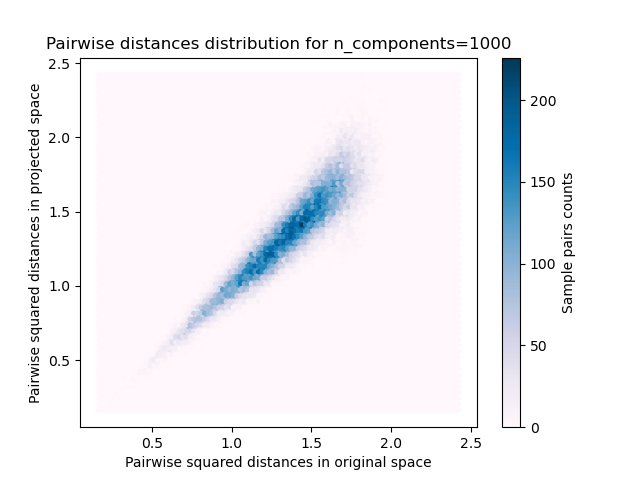
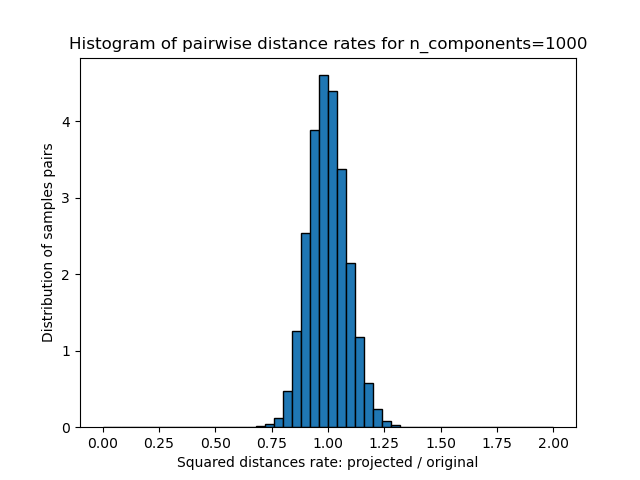
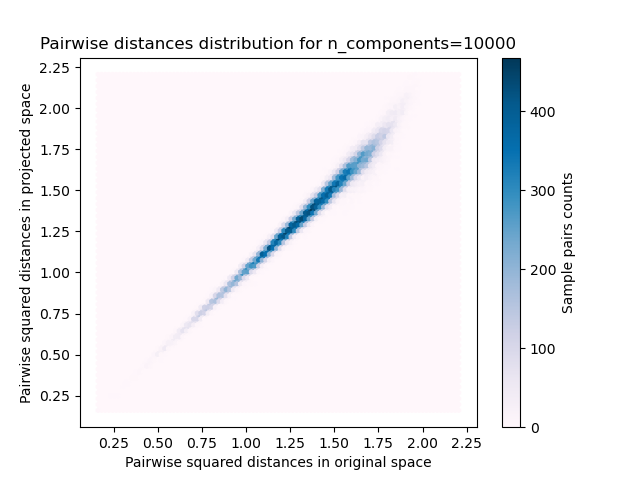
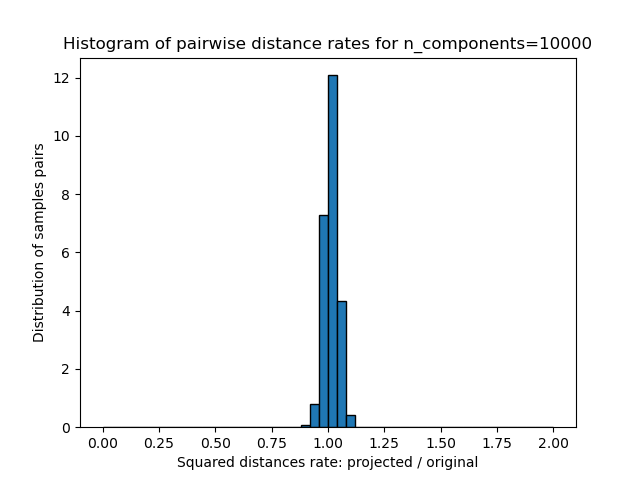
第二个图表明，允许失真的增加eps可以大大减少n_components给定数量样本的最小维数n_samples

根据JL引理，投影500个没有太多失真的样本将需要至少几千个维度，而不管原始数据集的特征数量。

因此，在输入空间中仅具有64个特征的数字数据集上使用随机投影是没有意义的：在这种情况下，它不允许降低维数。

另一方面，在二十个新闻组上，维度可以从56436降低到10000，同时合理地保留成对距离。

日期：

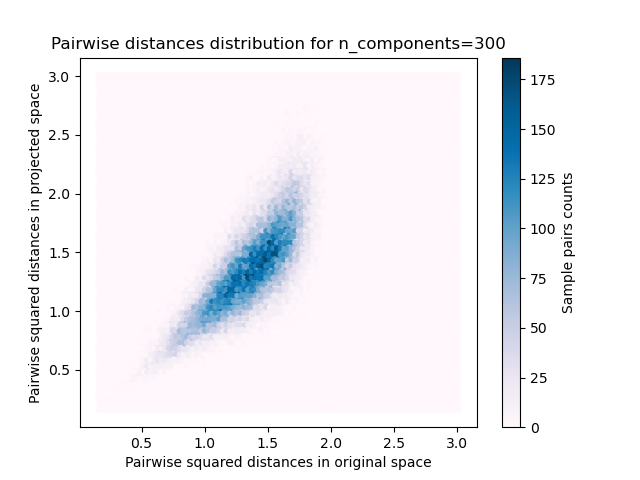
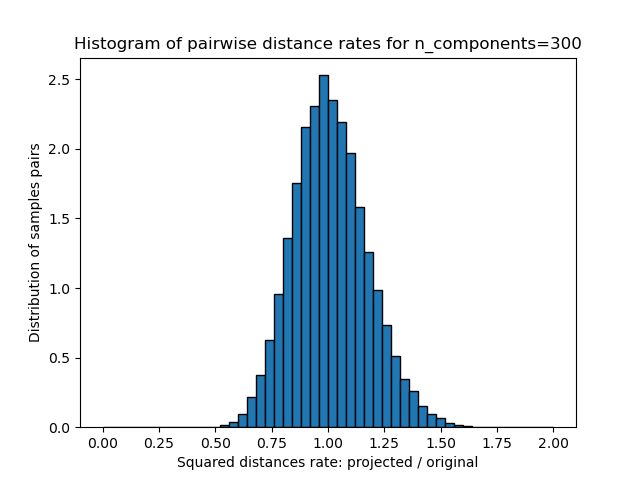
使用各种随机投影嵌入500个带有暗淡64的样本 预计500个样品从64到300个0.005s 随机矩阵，大小：0.029MB 平均距离率：1.02（0.09） 预计在0.014秒内从64到1000的500个样本 随机矩阵，大小：0.095MB 平均距离率：0.99（0.04） 预计在0.223秒内从64到10000的500个样本 随机矩阵，大小：0.962MB 平均距离率：1.00（0.02）