数据挖掘工程师笔试及答案整理

2013百度校园招聘数据挖掘工程师

《数据分析专项练习题库》

《CDA数据分析认证考试模拟题库》
《企业数据分析面试题库》

一、简答题（30分）
1、简述数据库操作的步骤（10分）

步骤：建立数据库连接、打开数据库连接、建立数据库命令、运行数据库命令、保存数据库命令、关闭数据库连接。

经萍萍提醒，了解到应该把preparedStatement预处理也考虑在数据库的操作步骤中。此外，对实时性要求不强时，可以使用数据库缓存。

2、TCP/IP的四层结构（10分）

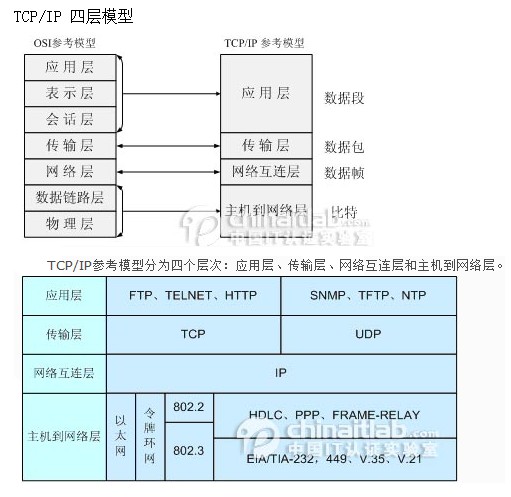
3、什么是MVC结构，简要介绍各层结构的作用（10分）

Model、view、control。

我之前有写过一篇《MVC层次的划分》

二、算法与程序设计（45分）
1、由a-z、0-9组成3位的字符密码，设计一个算法，列出并打印所有可能的密码组合（可用伪代码、C、C++、Java实现）（15分）

把a-z,0-9共（26+10）个字符做成一个数组，然后用三个for循环遍历即可。每一层的遍历都是从数组的第0位开始。

2、实现字符串反转函数（15分）

3、百度凤巢系统，广告客户购买一系列关键词，数据结构如下：（15分）
User1 手机 智能手机 iphone 台式机 …
User2 手机 iphone 笔记本电脑 三星手机 …
User3 htc 平板电脑 手机 …
（1）根据以上数据结构对关键词进行KMeans聚类，请列出关键词的向量表示、距离公式和KMeans算法的整体步骤

KMeans方法一个很重要的部分就是如何定义距离，而距离又牵扯到特征向量的定义，毕竟距离是对两个特征向量进行衡量。

本题中，我们建立一个table。

只要两个关键词在同一个user的描述中出现，我们就将它在相应的表格的位置加1.

这样我们就有了每个关键词的特征向量。

例如：

<手机>=（1,1,2,1,1,1,0,0）

<智能手机> = （1,1,1,1,0,0,0,0）

我们使用夹角余弦公式来计算这两个向量的距离。

夹角余弦公式：

设有两个向量a和b，，

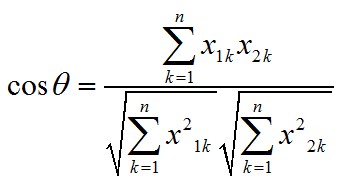
所以，cos<手机，智能机>=（1+1+2+1）/(sqrt(7+2^2)*sqrt(4))=0.75

cos<手机，iphone>=(2+1+2+1+1+1)/(sqrt(7+2^2)*sqrt(2^2+5))=0.80

夹角余弦值越大说明两者之间的夹角越小，夹角越小说明相关度越高。

通过夹角余弦值我们可以计算出每两个关键词之间的距离。

特征向量和距离计算公式的选择（还有其他很多种距离计算方式，各有其适应的应用场所）完成后，就可以进入KMeans算法。

KMeans算法有两个主要步骤：1、确定k个中心点；2、计算各个点与中心点的距离，然后贴上类标，然后针对各个类，重新计算其中心点的位置。

初始化时，可以设定k个中心点的位置为随机值，也可以全赋值为0。

KMeans的实现代码有很多，这里就不写了。

不过值得一提的是MapReduce模型并不适合计算KMeans这类递归型的算法，MR最拿手的还是流水型的算法。KMeans可以使用MPI模型很方便的计算（庆幸的是YARN中似乎开始支持MPI模型了），所以hadoop上现在也可以方便的写高效算法了（但是要是MRv2哦）。

（2）计算给定关键词与客户关键词的文字相关性，请列出关键词与客户的表达符号和计算公式

这边的文字相关性不知道是不是指非语义的相关性，而只是词频统计上的相关性？如果是语义相关的，可能还需要引入topic model来做辅助（可以看一下百度搜索研发部官方博客的这篇【语义主题计算】）……

如果是指词频统计的话，个人认为可以使用Jaccard系数来计算。

通过第一问中的表格，我们可以知道某个关键词的向量，现在将这个向量做一个简单的变化：如果某个分量不为0则记为1，表示包含这个分量元素，这样某个关键词就可以变成一些词语的集合，记为A。

客户输入的关键词列表也可以表示为一个集合，记为B

Jaccard系数的计算方法是：

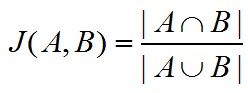
所以，假设某个用户userX的关键词表达为：{三星手机，手机，平板电脑}

那么，关键词“手机”与userX的关键词之间的相关性为：

J("手机"，“userX关键词”)=|{三星手机，手机，平板电脑}|/|{手机，智能手机，iphone，台式机，笔记本电脑，三星手机，HTC，平板电脑}| = 3/8

关键词“三星手机”与用户userX的关键词之间的相关性为：

J("三星手机"，“userX关键词”)=|{手机，三星手机}|/|{手机，三星手机，iphone，笔记本电脑，平板电脑}| = 2/5

三、系统设计题（25分）
一维数据的拟合，给定数据集{xi,yi}(i=1,…,n)，xi是训练数据，yi是对应的预期值。拟使用线性、二次、高次等函数进行拟合
线性：f(x)=ax+b
二次：f(x)=ax^2+bx+c
三次：f(x)=ax^3+bx^2+cx+d
（1）请依次列出线性、二次、三次拟合的误差函数表达式（2分）

误差函数的计算公式为：

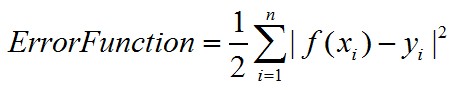
系数1/2只是为了之后求导的时候方便约掉而已。

那分别将线性、二次、三次函数带入至公式中f(xi)的位置，就可以得到它们的误差函数表达式了。
（2）按照梯度下降法进行拟合，请给出具体的推导过程。（7分）

假设我们样本集的大小为m，每个样本的特征向量为X1=(x11,x12, ..., x1n)。

那么整个样本集可以表示为一个矩阵：

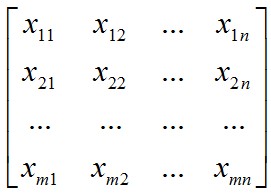其中每一行为一个样本向量。

我们假设系数为θ，则有系数向量：

对于第 i 个样本，我们定义误差变量为

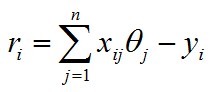
我们可以计算cost function：

由于θ是一个n维向量，所以对每一个分量求偏导：

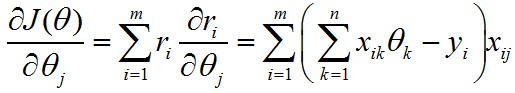
梯度下降的精华就在于下面这个式子：

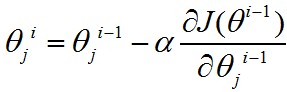
这个式子是什么意思呢？是将系数减去导数（导数前的系数先暂时不用理会），为什么是减去导数？我们看一个二维的例子。

假设有一个曲线如图所示：

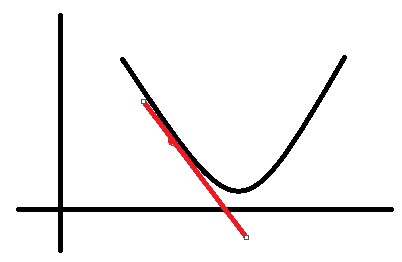
假设我们处在红色的点上，那么得到的导数是个负值。此时，我在当前位置（x轴）的基础上减去一个负值，就相当于加上了一个正值，那么就朝导数为0的位置移动了一些。

如果当前所处的位置是在最低点的右边，那么就是减去一个正值（导数为正），相当于往左移动了一些距离，也是朝着导数为0的位置移动了一些。

这就是梯度下降最本质的思想。

那么到底一次该移动多少呢？就是又导数前面的系数α来决定的。

现在我们再来看梯度下降的式子，如果写成矩阵计算的形式（使用隐式循环来实现），那么就有：

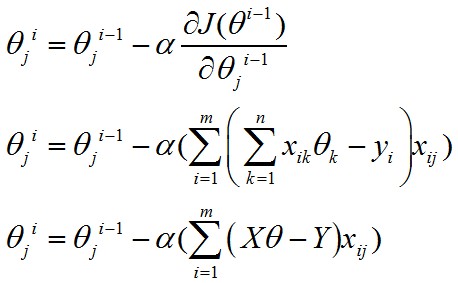
这边会有点棘手，因为j确定时，xij为一个数值（即，样本的第j个分量），Xθ-Y为一个m*1维的列向量（暂时称作“误差向量”）。

括号里面的部分就相当于：

第1个样本第j个分量*误差向量 + 第2个样本第j个分量*误差向量 + ... + 第m个样本第j个分量*误差向量

我们来考察一下式子中各个部分的矩阵形式。

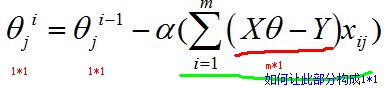
当j固定时，相当于对样本空间做了一个纵向切片，即：

那么此时的xij就是m*1向量，所以为了得到1*1的形式，我们需要拼凑 (1*m)*(m*1)的矩阵运算，因此有：

如果把θ向量的每个分量统一考虑，则有：

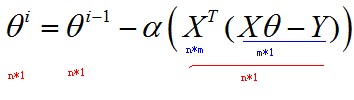
关于θ向量的不断更新的终止条件，一般以误差范围（如95%）或者迭代次数（如5000次）进行设定。

梯度下降的有点是：

不像矩阵解法那么需要空间（因为矩阵解法需要求矩阵的逆）

缺点是：如果遇上非凸函数，可能会陷入局部最优解中。对于这种情况，可以尝试几次随机的初始θ，看最后convergence时，得到的向量是否是相似的。

（3）下图给出了线性、二次和七次拟合的效果图。请说明进行数据拟合时，需要考虑哪些问题。在本例中，你选择哪种拟合函数。（8分）

因为是在网上找的题目，没有看到图片是长什么样。大致可能有如下几种情况。

如果是如上三幅图的话，当然是选择中间的模型。

欠拟合的发生一般是因为假设的模型过于简单。而过拟合的原因则是模型过于复杂且训练数据量太少。

对于欠拟合，可以增加模型的复杂性，例如引入更多的特征向量，或者高次方模型。

对于过拟合，可以增加训练的数据，又或者增加一个L2 penalty，用以约束变量的系数以实现降低模型复杂度的目的。

L2 penalty就是：

（注意不要把常数项系数也包括进来，这里假设常数项是θ0）

另外常见的penalty还有L1型的：

（L1型的主要是做稀疏化，即sparsity）

两者为什么会有这样作用上的区别可以找一下【统计之都】上的相关文章看一下。我也还没弄懂底层的原因是什么。

（4）给出实验方案（8分）

2013网易实习生招聘 岗位：数据挖掘工程师 
一、问答题 
a) 欠拟合和过拟合的原因分别有哪些？如何避免？

欠拟合：模型过于简单；过拟合：模型过于复杂，且训练数据太少。
b) 决策树的父节点和子节点的熵的大小？请解释原因。 

父节点的熵>子节点的熵

c) 衡量分类算法的准确率，召回率，F1值。

d) 举例序列模式挖掘算法有哪些？以及他们的应用场景。

DTW（动态事件规整算法）：语音识别领域，判断两端序列是否是同一个单词。

Holt-Winters（三次指数平滑法）：对时间序列进行预测。时间序列的趋势、季节性。

Apriori

Generalized Sequential Pattern(广义序贯模式)

PrefixSpan

二、计算题 
1) 给你一组向量a，b 
a) 计算二者欧氏距离 

(a-b)(a-b)T

即：

b) 计算二者曼哈顿距离 

2) 给你一组向量a，b，c，d
a) 计算a，b的Jaccard相似系数

b) 计算c，d的向量空间余弦相似度 

c) 计算c、d的皮尔森相关系数

即线性相关系数。

或者

三、（题目记得不是很清楚） 
一个文档-词矩阵，给你一个变换公式tfij’=tfij*log(m/dfi)；其中tfij代表单词i在文档f中的频率，m代表文档数，dfi含有单词i的文档频率。 
1) 只有一个单词只存在文档中，转换的结果？（具体问题忘记） 

2) 有多个单词存在在多个文档中，转换的结果？（具体问题忘记） 

3) 公式变换的目的？

四、推导朴素贝叶斯分类P(c|d)，文档d（由若干word组成），求该文档属于类别c的概率，
并说明公式中哪些概率可以利用训练集计算得到。

五、给你五张人脸图片。 
可以抽取哪些特征？按照列出的特征，写出第一个和最后一个用户的特征向量。

六、考查ID3算法，根据天气分类outlook/temperature/humidity/windy。（给你一张离散型
的图表数据，一般学过ID3的应该都知道） 

a) 哪一个属性作为第一个分类属性？ 

b) 画出二层决策树。 

七、购物篮事物（关联规则） 
一个表格：事物ID/购买项。 
1) 提取出关联规则的最大数量是多少？（包括0支持度的规则）

2) 提取的频繁项集的最大长度（最小支持>0） 

3) 找出能提取出4-项集的最大数量表达式 
4) 找出一个具有最大支持度的项集（长度为2或更大） 

5) 找出一对项a，b，使得{a}->{b}和{b}->{a}有相同置信度。

八、一个发布优惠劵的网站，如何给用户做出合适的推荐？有哪些方法？设计一个合适的系
统（线下数据处理，存放，线上如何查询？）