scikit-learn的线性回归模型-CDA数据分析师官网

scikit-learn的线性回归模型

2016-05-05

scikit-learn的线性回归模型

特征选择的方法

作为有监督学习，分类问题是预测类别结果，而回归问题是预测一个连续的结果。

1. 使用pandas来读取数据

Pandas是一个用于数据探索、数据处理、数据分析的Python库

In [1]:

importpandasaspd

In [2]:

# read csv file directly from a URL and save the resultsdata=pd.read_csv('http://www-bcf.usc.edu/~gareth/ISL/Advertising.csv',index_col=0)# display the first 5 rowsdata.head()

Out[2]:

	TV	Radio	Newspaper	Sales
1	230.1	37.8	69.2	22.1
2	44.5	39.3	45.1	10.4
3	17.2	45.9	69.3	9.3
4	151.5	41.3	58.5	18.5
5	180.8	10.8	58.4	12.9

上面显示的结果类似一个电子表格，这个结构称为Pandas的数据帧(data frame)。

pandas的两个主要数据结构：Series和DataFrame：

Series类似于一维数组，它有一组数据以及一组与之相关的数据标签(即索引)组成。

DataFrame是一个表格型的数据结构，它含有一组有序的列，每列可以是不同的值类型。DataFrame既有行索引也有列索引，它可以被看做由Series组成的字典。

In [3]:

# display the last 5 rowsdata.tail()

Out[3]:

	TV	Radio	Newspaper	Sales
196	38.2	3.7	13.8	7.6
197	94.2	4.9	8.1	9.7
198	177.0	9.3	6.4	12.8
199	283.6	42.0	66.2	25.5
200	232.1	8.6	8.7	13.4

In [4]:

# check the shape of the DataFrame(rows, colums)data.shape

Out[4]:

(200, 4)

特征：

TV：对于一个给定市场中单一产品，用于电视上的广告费用（以千为单位）

Radio：在广播媒体上投资的广告费用

Newspaper：用于报纸媒体的广告费用

响应：

Sales：对应产品的销量

在这个案例中，我们通过不同的广告投入，预测产品销量。因为响应变量是一个连续的值，所以这个问题是一个回归问题。数据集一共有200个观测值，每一组观测对应一个市场的情况。

In [5]:

importseabornassns%matplotlibinline

In [6]:

# visualize the relationship between the features and the response using scatterplotssns.pairplot(data,x_vars=['TV','Radio','Newspaper'],y_vars='Sales',size=7,aspect=0.8)

Out[6]:

<seaborn.axisgrid.PairGrid at 0x82dd890>

seaborn的pairplot函数绘制X的每一维度和对应Y的散点图。通过设置size和aspect参数来调节显示的大小和比例。可以从图中看出，TV特征和销量是有比较强的线性关系的，而Radio和Sales线性关系弱一些，Newspaper和Sales线性关系更弱。通过加入一个参数kind=’reg’，seaborn可以添加一条最佳拟合直线和95%的置信带。

In [7]:

sns.pairplot(data,x_vars=['TV','Radio','Newspaper'],y_vars='Sales',size=7,aspect=0.8,kind='reg')

Out[7]:

<seaborn.axisgrid.PairGrid at 0x83b76f0>

2. 线性回归模型

优点：快速；没有调节参数；可轻易解释；可理解

缺点：相比其他复杂一些的模型，其预测准确率不是太高，因为它假设特征和响应之间存在确定的线性关系，这种假设对于非线性的关系，线性回归模型显然不能很好的对这种数据建模。

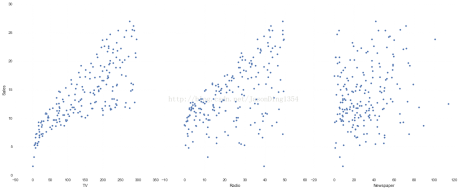
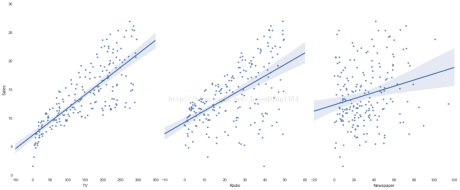
线性模型表达式： y=β0+β1x1+β2x2+...+βnxn 其中

y是响应

β0是截距

β1是x1的系数，以此类推

在这个案例中： y=β0+β1∗TV+β2∗Radio+...+βn∗Newspaper

（1）使用pandas来构建X和y

scikit-learn要求X是一个特征矩阵，y是一个NumPy向量

pandas构建在NumPy之上

因此，X可以是pandas的DataFrame，y可以是pandas的Series，scikit-learn可以理解这种结构

In [8]:

# create a python list of feature namesfeature_cols=['TV','Radio','Newspaper']# use the list to select a subset of the original DataFrameX=data[feature_cols]# equivalent command to do this in one lineX=data[['TV','Radio','Newspaper']]# print the first 5 rowsX.head()

Out[8]:

	TV	Radio	Newspaper
1	230.1	37.8	69.2
2	44.5	39.3	45.1
3	17.2	45.9	69.3
4	151.5	41.3	58.5
5	180.8	10.8	58.4

In [9]:

# check the type and shape of Xprinttype(X)printX.shape

<class 'pandas.core.frame.DataFrame'> (200, 3)

In [10]:

# select a Series from the DataFramey=data['Sales']# equivalent command that works if there are no spaces in the column namey=data.Sales# print the first 5 valuesy.head()

Out[10]:

1 22.1 2 10.4 3 9.3 4 18.5 5 12.9 Name: Sales, dtype: float64

In [11]:

printtype(y)printy.shape

<class 'pandas.core.series.Series'> (200,)

(2)构造训练集和测试集

In [12]:

fromsklearn.cross_validationimporttrain_test_splitX_train,X_test,y_train,y_test=train_test_split(X,y,random_state=1)

In [14]:

# default split is 75% for training and 25% for testingprintX_train.shapeprinty_train.shapeprintX_test.shapeprinty_test.shape

(150, 3) (150,) (50, 3) (50,)

(3)Scikit-learn的线性回归

In [15]:

fromsklearn.linear_modelimportLinearRegressionlinreg=LinearRegression()linreg.fit(X_train,y_train)

Out[15]:

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)

In [16]:

printlinreg.intercept_printlinreg.coef_

2.87696662232 [ 0.04656457 0.17915812 0.00345046]

In [17]:

# pair the feature names with the coefficientszip(feature_cols,linreg.coef_)

Out[17]:

[('TV', 0.046564567874150253), ('Radio', 0.17915812245088836), ('Newspaper', 0.0034504647111804482)]

y=2.88+0.0466∗TV+0.179∗Radio+0.00345∗Newspaper

如何解释各个特征对应的系数的意义？

对于给定了Radio和Newspaper的广告投入，如果在TV广告上每多投入1个单位，对应销量将增加0.0466个单位

更明确一点，加入其它两个媒体投入固定，在TV广告上没增加1000美元（因为单位是1000美元），销量将增加46.6（因为单位是1000）

(4)预测

In [18]:

y_pred=linreg.predict(X_test)

3. 回归问题的评价测度

对于分类问题，评价测度是准确率，但这种方法不适用于回归问题。我们使用针对连续数值的评价测度(evaluation metrics)。

下面介绍三种常用的针对回归问题的评价测度

In [21]:

# define true and predicted response valuestrue=[100,50,30,20]pred=[90,50,50,30]

(1)平均绝对误差(Mean Absolute Error, MAE)

1n∑ni=1|yi−yi^|

(2)均方误差(Mean Squared Error, MSE)

1n∑ni=1(yi−yi^)2

(3)均方根误差(Root Mean Squared Error, RMSE)

1n∑ni=1(yi−yi^)2−−−−−−−−−−−−−√

In [24]:

fromsklearnimportmetricsimportnumpyasnp# calculate MAE by handprint"MAE by hand:",(10+0+20+10)/4.# calculate MAE using scikit-learnprint"MAE:",metrics.mean_absolute_error(true,pred)# calculate MSE by handprint"MSE by hand:",(10**2+0**2+20**2+10**2)/4.# calculate MSE using scikit-learnprint"MSE:",metrics.mean_squared_error(true,pred)# calculate RMSE by handprint"RMSE by hand:",np.sqrt((10**2+0**2+20**2+10**2)/4.)# calculate RMSE using scikit-learnprint"RMSE:",np.sqrt(metrics.mean_squared_error(true,pred))

MAE by hand: 10.0 MAE: 10.0 MSE by hand: 150.0 MSE: 150.0 RMSE by hand: 12.2474487139 RMSE: 12.2474487139

计算Sales预测的RMSE

In [26]:

printnp.sqrt(metrics.mean_squared_error(y_test,y_pred))

1.40465142303

4. 特征选择

在之前展示的数据中，我们看到Newspaper和销量之间的线性关系比较弱，现在我们移除这个特征，看看线性回归预测的结果的RMSE如何？

In [27]:

feature_cols=['TV','Radio']X=data[feature_cols]y=data.SalesX_train,X_test,y_train,y_test=train_test_split(X,y,random_state=1)linreg.fit(X_train,y_train)y_pred=linreg.predict(X_test)printnp.sqrt(metrics.mean_squared_error(y_test,y_pred))

1.38790346994

我们将Newspaper这个特征移除之后，得到RMSE变小了，说明Newspaper特征不适合作为预测销量的特征，于是，我们得到了新的模型。我们还可以通过不同的特征组合得到新的模型，看看最终的误差是如何的。

CDA数据分析师考试相关入口一览（建议收藏）：

▷ 想报名CDA认证考试，点击>>> “CDA报名” 了解CDA考试详情；

▷ 想加入CDA考试题库，点击>>> “CDA题库” 了解CDA考试详情；

▷ 想学习CDA考试教材，点击>>> “CDA教材” 了解CDA考试详情；

▷ 想查询CDA考试成绩，点击>>> “CDA成绩” 了解CDA考试详情；

▷ 想了解CDA考试含金量，点击>>> “CDA含金量” 了解CDA考试详情；

▷ 想获取CDA考试时间/费用/条件/大纲/通过率，点击 >>>“CDA考试官网” 了解CDA考试详情；

特征 pandas DataFrame Series 线性回归 seaborn 有监督散点图

数据分析咨询请扫描二维码

若不方便扫码，搜微信号：CDAshujufenxi

上一篇图论在大数据分析中的作用！

下一篇CDA认证再升一档！与国家共同推进大数据人才培养标准教育事业！

scikit-learn的线性回归模型

1. 使用pandas来读取数据

2. 线性回归模型

（1）使用pandas来构建X和y

scikit-learn要求X是一个特征矩阵，y是一个NumPy向量

pandas构建在NumPy之上

因此，X可以是pandas的DataFrame，y可以是pandas的Series，scikit-learn可以理解这种结构

(2)构造训练集和测试集

(3)Scikit-learn的线性回归

(4)预测

3. 回归问题的评价测度

计算Sales预测的RMSE

4. 特征选择

CDA考试动态

CDA报考指南

热门栏目

最新资讯

excel没有数据分析怎么添加

转行数据分析师就是找死

python可视化数据分析

用数据还是靠经验？成功企业都找到了这个平衡点！ ...

Spark SQL 结构化数据处理流程及原理是什么？ ...

数据分析岗位是干什么的

字节大神：讲透数据指标体系搭建的3个关键步骤 ...

提升思维能力！数据分析必学的5大经典模型解析！ ...

数据分析师的工作内容

【干货】互联网黑话多？谁说这术语老啊？这术语太棒 ...

数据分析包括哪些内容

【干货】数分人年终述职指南：解锁高效汇报秘籍 ...

【干货】竞品分析怎么写？戳此了解深度指南！ ...

数据分析的终极对决：大数据还是小数据，谁才是真正 ...

如何做数据分析图表

数据分析师就业前景

字节70W年薪数据分析师：数据分析报告撰写的4个要点 ...

数据分析的基本流程

数据分析岗位需要什么技能

数据分析师会成为下一个失业高危职业吗？ ...