数据分析之_离群值（Outliers） BoxPlot_数据分析师

一：什么是Outliers

Outliers是统计学专业术语，是指相比一组数据中的其它数据的极限值

 

二：极限值意味什么

 1. 决定哪些值是Outliers是一个主观行为，有一些基准数据来决定是否一个值是一个Outliers，这些基准是任意选择的，比如P<=0.5就是一个任意选择的基准

2. 一个基准是用BoxPlot来决定适度离群值（mild Outliers）和极限离群值（extreme Outliers），适度离群值是任何值1.5倍大于基于剩下所有的值的IQR，极限离群值是任何值3倍大于剩下所有的值的IQR，IQR（Interquartile Range）代表四分位数间距，是这些值中的50%中间值，分别是Q1-25%, Median-50%,Q3-75%, IQR=Q3-Q1

 

三：使用Box Plot来发现Outliers

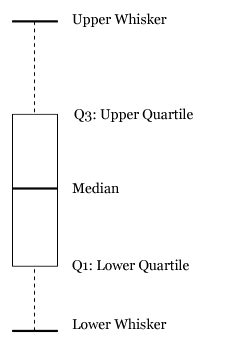
一个典型的Box Plot是基于以下五个值计算而来的

a. 一组样本的最小值

b. 一组样本的最大值

c. 一组样本的中值

d. 下四分位数（Lower Quartile / Q1）

e. 上四分位数（Upper Quartile / Q3）

根据这五个值构建出来基本的Box Plot，某些图形软件还会显示平均值，IQR= Q3 – Q1

显然超出上下四分位数的值可以看做为Outliers。我们通过眼睛就可以很好的观察到这些Outliers值的点。

 

一个显示适度和极限Outliers值的Box plot显示如下：

四：示例说明及JfreeChart的实现

假设一组数据为：2,4,6,8,12,14,16,18,20,25,45

中值 Median = 14

Q1-下四分位数（11 * 0.25 = 3） = 7

Q3-上四分位数（11 * 0.75 = 9） =19

IQR（Q3 – Q1） = 12

1.5 * IQR = 18

最小值（6 – 1.5 * IQR）= 2

最大值（20 + 1.5 * IQR）= 25

很显然值45是一个适度Outliers

对比的一组数据为：2,4,6,8,12,14,16,18,20,25,26

 

 

从图上可以看出Series0的数据存在Outliers，一个红色三角形已经表明

同样Series1的数据是一组非常好的数据，没有Outliers.

 

下面是Java源代码：

package com.dataanalysis.plots; import java.awt.Font; import java.util.ArrayList; import java.util.List; import org.jfree.chart.ChartPanel; import org.jfree.chart.JFreeChart; import org.jfree.chart.axis.CategoryAxis; import org.jfree.chart.axis.NumberAxis; import org.jfree.chart.labels.BoxAndWhiskerToolTipGenerator; import org.jfree.chart.plot.CategoryPlot; import org.jfree.chart.renderer.category.BoxAndWhiskerRenderer; import org.jfree.data.statistics.BoxAndWhiskerCategoryDataset; import org.jfree.data.statistics.DefaultBoxAndWhiskerCategoryDataset; import org.jfree.ui.ApplicationFrame; import org.jfree.ui.RefineryUtilities; public class BoxAndWhiskerDemo extends ApplicationFrame {     /** *   */ private static final long serialVersionUID = -3205574763811416266L;     /**      * Creates a new demo.      *      * @param title  the frame title.      */     public BoxAndWhiskerDemo(final String title) {         super(title);                  final BoxAndWhiskerCategoryDataset dataset = createSampleDataset();         final CategoryAxis xAxis = new CategoryAxis("Type");         final NumberAxis yAxis = new NumberAxis("Value");         yAxis.setAutoRangeIncludesZero(false);         final BoxAndWhiskerRenderer renderer = new BoxAndWhiskerRenderer();         renderer.setFillBox(false);         renderer.setToolTipGenerator(new BoxAndWhiskerToolTipGenerator());         final CategoryPlot plot = new CategoryPlot(dataset, xAxis, yAxis, renderer);         final JFreeChart chart = new JFreeChart(             "Box-and-Whisker Demo",             new Font("SansSerif", Font.BOLD, 14),             plot,             true         );         final ChartPanel chartPanel = new ChartPanel(chart);         chartPanel.setPreferredSize(new java.awt.Dimension(450, 270));         setContentPane(chartPanel);     }     /**      * Creates a sample dataset.      *       * @return A sample dataset.      */     private BoxAndWhiskerCategoryDataset createSampleDataset() {                  final int seriesCount = 2;         final int categoryCount = 4;         double[] data = null;         final DefaultBoxAndWhiskerCategoryDataset dataset              = new DefaultBoxAndWhiskerCategoryDataset();         for (int i = 0; i < seriesCount; i++) {         if(i == 0) {         data = new double[]{2,4,6,8,12,14,16,18,20,25,45};         } else {         data = new double[]{2,4,6,8,12,14,16,18,20,25,26};         }                     for (int j = 0; j < categoryCount; j++) {                 final List list = new ArrayList();                 for (int k = 0; k < data.length; k++) {                     list.add(new Double(data[k]));                 }                 dataset.add(list, "Series " + i, " Type " + j);             }                      }         return dataset;     }     /**      * For testing from the command line.      *      * @param args  ignored.      */     public static void main(final String[] args) {         final BoxAndWhiskerDemo demo = new BoxAndWhiskerDemo("Box-and-Whisker Chart Demo");         demo.pack();         RefineryUtilities.centerFrameOnScreen(demo);         demo.setVisible(true);     } }