决策树算法真的越复杂越好吗?
凡是在统计分析或机器学习领域从业的朋友们,对决策树这个名词肯定都不陌生吧。
决策树是一种解决分类问题的绝好方法,顾名思义,它正像一棵大树一样,由根部不断生长出很多枝叶;它的优点实在太多,比如可以避免缺失值的影响、可以处理混合预测、模型容易展示等。然而,决策树的实际应用也绝不简单,如果树根稍有不稳、或者枝干略有差池,树就可能会彻底长偏啦,我们总是需要仔细挑选单棵决策树、或适当的组合。
单棵决策树
这是统计分析领域比较常用、机器学习领域也用得烂熟的分类算法:一棵大树上每支叶子自成一类。在实际业务中,大家最关心的问题包括:在每一个节点该选择哪个属性进行分割?该怎样分割才能效果最好?这些问题通常都可以通过SAS Enterprise Miner中强大的交互决策树功能解决,选择最大的logworth值来选择拆分变量、创建拆分规则。
不过,这样的分类过程到底应该在什么时候结束呢?最直观的方式当然是在每个子节点只有一种类型的记录时停止分类,但是这样可能会使得树的节点过多,导致过拟合问题(overfitting),即该决策树对训练数据可以得到很低的错误率,但是运用到验证数据上时却错误率极高。所以,剪枝是优化和解决这类问题的必要做法,我们之前介绍过的K折交叉验证(点击阅读)也可用来对原始决策树进行验证和裁减,从而得到最优决策树。单棵决策树的实现在SAS Enterprise Miner中有现成的节点可直接使用。
除了剪枝、交叉验证等手段外,为了有效减少单决策树带来的问题,与决策树相关的组合分类(比如Bagging, Boosting等算法)也逐渐被引入进来,这些算法的精髓都是通过生成N棵树(N可能高达几百)、最终形成一棵最适合的结果分类树。有人戏称这是三个臭皮匠顶一个诸葛亮的算法:虽然这几百棵决策树中的每一棵相对于C4.5算法来说可能都很简单,但是他们组合起来却真的很强大。下面我们就来简单介绍几种常见的组合算法:
Bagging组合算法
Bagging组合算法是bootstrap aggregating的缩写。我们可以让上述决策树学习算法训练多轮,每轮的训练集由从初始的训练集中有放回地随机抽取n个训练样本组成,某个初始训练样本在某轮训练集中可以出现多次或根本不出现,训练之后就可以得到一个决策树群h_1,……h_n ,也类似于一个森林。最终的决策树H对分类问题采用投票方式,对回归问题采用简单平均方法对新示例进行判别。
Boosting组合算法
此类算法中其中应用最广的是AdaBoost(Adaptive Boosting)。在此算法中,初始化时以等权重有放回抽样方式进行训练,接下来每次训练后要特别关注前一次训练失败的训练样本,并赋以较大的权重进行抽样,从而得到一个预测函数序列h_1,⋯, h_m , 其中h_i也有一定的权重,预测效果好的预测函数权重较大,反之较小。最终的预测函数H对分类问题采用有权重的投票方式,所以Boosting更像是一个人学习的过程,刚开始学习时会做一些习题,常常连一些简单的题目都会弄错,但经过对这些题目的针对性练习之后,解题能力自然会有所上升,就会去做更复杂的题目;等到他完成足够多题目后,不管是难题还是简单题都可以解决掉了。
随机森林(Random forest)
随机森林,顾名思义,是用随机的方式建立一个森林,所以它对输入数据集要进行行、列的随机采样。行采样采用有放回的随机抽样方式,即采样样本中可能有重复的记录;列采样就是随机抽取部分分类特征,然后使用完全分裂的方式不断循环建立决策树群。当有新的输入样本进入的时候,也要通过投票方式决定最终的分类器。
一般的单棵决策树都需要进行剪枝操作,但随机森林在经过两个随机采样后,就算不剪枝也不会出现overfitting。我们可以这样比喻随机森林算法:从M个feature中选择m个让每一棵决策树进行学习时,就像是把它们分别培养成了精通于某一个窄领域的专家,因此在随机森林中有很多个不同领域的专家,对一个新的问题(新的输入数据)可以从不同的角度去看待,最终由各位专家投票得到结果。
至此,我们已经简单介绍了各类算法的原理,这些组合算法们看起来都很酷炫。可是它们之间究竟有哪些差异呢?
随机森林与Bagging算法的区别主要有两点:
Boosting和Bagging算法之间的主要区别是取样方式的不同。Bagging采用均匀取样,而Boosting根据错误率来取样,因此Boosting的分类精度要优于Bagging。Bagging和Boosting都可以有效地提高分类的准确性。在多数数据集中,Boosting的准确性比Bagging高一些,不过Boosting在某些数据集中会引起退化——过拟合。
俗话说三个臭皮匠赛过诸葛亮,各类组合算法的确有其优越之处;我们也认为,模型效果从好到差的排序通常依次为:随机森林>Boosting > Bagging > 单棵决策树。但归根结底,这只是一种一般性的经验、而非定论,应根据实际数据情况具体分析。就单棵决策树和组合算法相比较而言,决策树相关的组合算法在提高模型区分能力和预测精度方面比较有效,对于像决策树、神经网络这样的“不稳定”算法有明显的提升效果,所以有时会表现出优于单棵决策树的效果。但复杂的模型未必一定是最好的,我们要在具体的分析案例中,根据业务需求和数据情况在算法复杂性和模型效果之间找到平衡点。
下面就通过一个实际案例来说明我们的观点吧。在笔者多年的数据分析工作中,无论哪种分析都难以离开钟爱的SAS Enterprise Miner软件,这里我们也以SAS EM来实现各分类算法在实际案例中的具体应用和分类效果。
本文使用的样例数据是一组2015年第三季度的房屋贷款数据,大约共5960条数据,其中贷款逾期的客户数占比为19.95%, 分析变量包含所需的贷款金额、贷款客户的职业类别、当前工作年限、押品的到期价值等13个属性特征。我们的目标是要通过上述数据来拟合贷款客户是否会出现逾期行为的分类模型,进而判断和预测2015年第四季度的房贷客户是否会出现逾期情况。
在建立各类模型前,笔者同样利用数据分区节点将全量的建模样本一分为二,其中70%作为训练样本、30%作为验证样本,然后再来逐个建立、验证决策树的单棵树模型和组合分类模型,并进行模型之间的比较分析和评估。
模型建设和分析的整个流程图逻辑如下:

熟悉SAS EM的小伙伴会发现,三种组合算法都使用了开始组这样的节点,目的有三:
传统的Bagging和Boosting算法在操作中都需要在开始组节点中设置属性;
对于随机森林的实现,可添加SAS code节点通过手工coding方式实现随机森林;
对不同算法设置尽可能相同的模型属性,方便比较模型预测效果,比如组合算法中循环次数都选择为10次。
说到这里,大家大概迫不及待要看看四类模型对新样本的预测准确性了吧,下图就是利用上述四种分类模型对2015年第四季度房贷新样本客户的贷款逾期情况的预测概率分布结果:
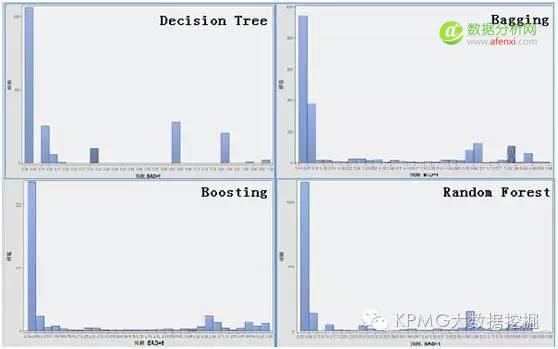
四张图中分别是单棵决策树、Bagging算法、Boosting算法和随机森林算法的结果。图中的横轴代表逾期概率,纵轴代表客户数量,显然,高柱状分布越是靠向右边,说明预测得到逾期客户越多;高柱状分布越是靠向左边,说明贷款客户信用较好。整体来看,新样本中预期逾期客户较少,但也有一部分客户比较集中地分布在逾期概率为0.7和0.85附近,这些客户需要特别关注。
对于这样的分类结果,又如何来判断它的预测准确性是好是差呢?这时就要推出误分类率和和均方误差这两个统计量了。从下面的结果可以看出,四类模型的误分类率都很小,相比较而言,单棵决策树最终胜出。
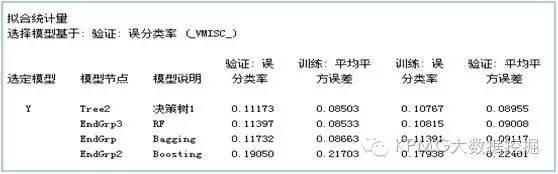
是不是完全没想到?上文看起来不太高大上的单棵决策树,在这个案例中倒是效果格外好。再来看看其他统计量的比较吧:


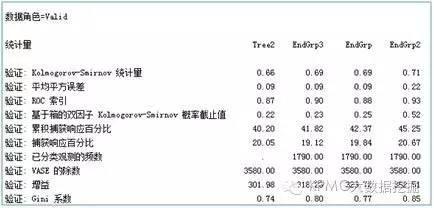
从上面的结果看,四类模型中ROC统计量的值都在0.8以上,KS值也都在0.6以上,说明它们的效果都比较好。我们使用的样本数据分布本身较为理想,单决策树模型的效果已经就相当理想,即使使用其他组合算法进行优化,模型效果的差异不会太明显,而三类组合算法之间的差异也不太突出。
我们同时发现,组合算法在提升度上确实比单个决策树效果要好,尤其Boosting算法表现更为明显。但是SAS EM的模型比较节点还是认为单决策树模型是最优模型,其验证集误判率最小。
就这一案例而言,尽管单决策树模型的区分能力和提升度都没有Boosting算法和随机森林算法效果好,但其本身的效果已经在合理且效果较好的范围之内了,而且模型本身运行效率较高、可解释性也很高。组合算法虽然看起来更厉害,但在应用实际业务场景和实际数据分布时,找到模型复杂度和模型效果之间的平衡取舍也是需要慎重考虑的。
我一向认为,一名数据分析工作者的重要素质不但在于深入掌握多种方法,更在于做出合适的选择,为不同的业务情境选择最恰当的方法。毕竟,没有哪种算法是解决所有问题的万灵药,而模型的运行效率、甚至可解释性等评判指标,在实际工作中可能与模型效果同等重要。复杂未必一定优于简单,而真正考验功力的,永远是化繁为简。

数据分析咨询请扫描二维码
若不方便扫码,搜微信号:CDAshujufenxi
持证人简介:贺渲雯 ,CDA 数据分析师一级持证人,互联网行业数据分析师 今天我将为大家带来一个关于用户私域用户质量数据分析 ...
2025-04-18一、CDA持证人介绍 在数字化浪潮席卷商业领域的当下,数据分析已成为企业发展的关键驱动力。为助力大家深入了解数据分析在电商行 ...
2025-04-17CDA持证人简介:居瑜 ,CDA一级持证人,国企财务经理,13年财务管理运营经验,在数据分析实践方面积累了丰富的行业经验。 一、 ...
2025-04-16持证人简介: CDA持证人刘凌峰,CDA L1持证人,微软认证讲师(MCT)金山办公最有价值专家(KVP),工信部高级项目管理师,拥有 ...
2025-04-15持证人简介:CDA持证人黄葛英,ICF国际教练联盟认证教练,前字节跳动销售主管,拥有丰富的行业经验。在实际生活中,我们可能会 ...
2025-04-14在 Python 编程学习与实践中,Anaconda 是一款极为重要的工具。它作为一个开源的 Python 发行版本,集成了众多常用的科学计算库 ...
2025-04-14随着大数据时代的深入发展,数据运营成为企业不可或缺的岗位之一。这个职位的核心是通过收集、整理和分析数据,帮助企业做出科 ...
2025-04-11持证人简介:CDA持证人黄葛英,ICF国际教练联盟认证教练,前字节跳动销售主管,拥有丰富的行业经验。 本次分享我将以教培行业为 ...
2025-04-11近日《2025中国城市长租市场发展蓝皮书》(下称《蓝皮书》)正式发布。《蓝皮书》指出,当前我国城市住房正经历从“增量扩张”向 ...
2025-04-10在数字化时代的浪潮中,数据已经成为企业决策和运营的核心。每一位客户,每一次交易,都承载着丰富的信息和价值。 如何在海量客 ...
2025-04-09数据是数字化的基础。随着工业4.0的推进,企业生产运作过程中的在线数据变得更加丰富;而互联网、新零售等C端应用的丰富多彩,产 ...
2025-04-094月7日,美国关税政策对全球金融市场的冲击仍在肆虐,周一亚市早盘,美股股指、原油期货、加密货币、贵金属等资产齐齐重挫,市场 ...
2025-04-08背景 3月26日,科技圈迎来一则重磅消息,苹果公司宣布向浙江大学捐赠 3000 万元人民币,用于支持编程教育。 这一举措并非偶然, ...
2025-04-07在当今数据驱动的时代,数据分析能力备受青睐,数据分析能力频繁出现在岗位需求的描述中,不分岗位的任职要求中,会特意标出“熟 ...
2025-04-03在当今数字化时代,数据分析师的重要性与日俱增。但许多人在踏上这条职业道路时,往往充满疑惑: 如何成为一名数据分析师?成为 ...
2025-04-02最近我发现一个绝招,用DeepSeek AI处理Excel数据简直太爽了!处理速度嘎嘎快! 平常一整天的表格处理工作,现在只要三步就能搞 ...
2025-04-01你是否被统计学复杂的理论和晦涩的公式劝退过?别担心,“山有木兮:统计学极简入门(Python)” 将为你一一化解这些难题。课程 ...
2025-03-31在电商、零售、甚至内容付费业务中,你真的了解你的客户吗? 有些客户下了一两次单就消失了,有些人每个月都回购,有些人曾经是 ...
2025-03-31在数字化浪潮中,数据驱动决策已成为企业发展的核心竞争力,数据分析人才的需求持续飙升。世界经济论坛发布的《未来就业报告》, ...
2025-03-28你有没有遇到过这样的情况?流量进来了,转化率却不高,辛辛苦苦拉来的用户,最后大部分都悄无声息地离开了,这时候漏斗分析就非 ...
2025-03-27