回归诊断主要内容
(1).误差项是否满足独立性，等方差性与正态
(2).选择线性模型是否合适
(3).是否存在异常样本
(4).回归分析是否对某个样本的依赖过重，也就是模型是否具有稳定性
(5).自变量之间是否存在高度相关，是否有多重共线性现象存在
通过了t检验与F检验，但是做为回归方程还是有问题
#举例说明，利用anscombe数据
## 调取数据集
data(anscombe)
## 分别调取四组数据做回归并输出回归系数等值
ff <- y ~ x
for(i in 1:4) {
ff[2:3] <- lapply(paste(c("y","x"), i, sep=""), as.name)
assign(paste("lm.",i,sep=""), lmi<-lm(ff, data=anscombe))
}
GetCoef<-function(n) summary(get(n))$coef
lapply(objects(pat="lm\\.[1-4]$"), GetCoef)
[[1]]
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.0000909 1.1247468 2.667348 0.025734051
x1 0.5000909 0.1179055 4.241455 0.002169629
[[2]]
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.000909 1.1253024 2.666758 0.025758941
x2 0.500000 0.1179637 4.238590 0.002178816
[[3]]
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.0024545 1.1244812 2.670080 0.025619109
x3 0.4997273 0.1178777 4.239372 0.002176305
[[4]]
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.0017273 1.1239211 2.670763 0.025590425
x4 0.4999091 0.1178189 4.243028 0.002164602
从计算结果可以知道，Estimate， Std. Error， t value， Pr(>|t|)这几个值完全不同，并且通过检验，进一步发现R^2,F值，p值完全相同，方差完全相同。事实上这四组数据完全不同，全部用线性回归不合适。
## 绘图
op <- par(mfrow=c(2,2), mar=.1+c(4,4,1,1), oma=c(0,0,2,0))
for(i in 1:4) {
ff[2:3] <- lapply(paste(c("y","x"), i, sep=""), as.name)
plot(ff, data =anscombe, col="red", pch=21,
bg="orange", cex=1.2, xlim=c(3,19), ylim=c(3,13))
abline(get(paste("lm.",i,sep="")), col="blue")
}
mtext("Anscombe's 4 Regression data sets",
outer = TRUE, cex=1.5)
par(op)
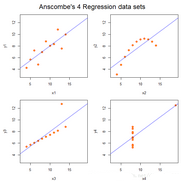
第1组数据适用于线性回归模型，第二组使用二次模型更加合理，第三组的一个点偏离于整体数据构成的回归直线，应该去掉。第四级做回归是不合理的，回归系只依赖一个点。在得到回归方程得到各种检验后，还要做相关的回归诊断。
残差检验
残差的检验是检验模型的误差是否满足正态性和方差齐性，最简单直观的方法是画出残差图。观察残差分布情况，作出散点图。
#20-60岁血压与年龄分析
## (1) 回归
rt<-read.table("d:/R-TT/book1/1_R/chap06/blood.dat", header=TRUE)
lm.sol<-lm(Y~X, data=rt); lm.sol
summary(lm.sol)
Call:
lm(formula = Y ~ X, data = rt)
Residuals:
Min 1Q Median 3Q Max
-16.4786 -5.7877 -0.0784 5.6117 19.7813
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 56.15693 3.99367 14.061 < 2e-16 ***
X 0.58003 0.09695 5.983 2.05e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 8.146 on 52 degrees of freedom
Multiple R-squared: 0.4077, Adjusted R-squared: 0.3963
F-statistic: 35.79 on 1 and 52 DF, p-value: 2.05e-07
## (2) 残差图
pre<-fitted.values(lm.sol)
#fitted value 配适值；拟合值
res<-residuals(lm.sol)
#计算回归模型的残差
rst<-rstandard(lm.sol)
#计算回归模型标准化残差
par(mai=c(0.9, 0.9, 0.2, 0.1))
plot(pre, res, xlab="Fitted Values", ylab="Residuals")
savePlot("resid-1", type="eps")
plot(pre, rst, xlab="Fitted Values",
ylab="Standardized Residuals")
savePlot("resid-2", type="eps")
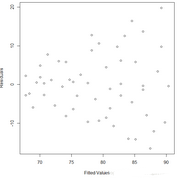
残差
标准差
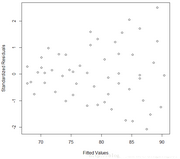
## (3) 对残差作回归,利用残差绝对值与自变量（x）作回归，其程序如下：
rt$res<-res
lm.res<-lm(abs(res)~X, data=rt); lm.res
summary(lm.res)
Call:
lm(formula = abs(res) ~ X, data = rt)
Residuals:
Min 1Q Median 3Q Max
-9.7639 -2.7882 -0.1587 3.0757 10.0350
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.54948 2.18692 -0.709 0.48179
X 0.19817 0.05309 3.733 0.00047 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.461 on 52 degrees of freedom
Multiple R-squared: 0.2113, Adjusted R-squared: 0.1962
F-statistic: 13.93 on 1 and 52 DF, p-value: 0.0004705
si= -1.5495 + 0.1982x
## (4) 计算残差的标准差,利用方差（标准差的平方）的倒数作为样本点的权重，这样可以减少非齐性方差带来的影响
s<-lm.res$coefficients[1]+lm.res$coefficients[2]*rt$X
lm.weg<-lm(Y~X, data=rt, weights=1/s^2); lm.weg
summary(lm.weg)
Call:
lm(formula = Y ~ X, data = rt, weights = 1/s^2)
Weighted Residuals:
Min 1Q Median 3Q Max
-2.0230 -0.9939 -0.0327 0.9250 2.2008
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 55.56577 2.52092 22.042 < 2e-16 ***
X 0.59634 0.07924 7.526 7.19e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.213 on 52 degrees of freedom
Multiple R-squared: 0.5214, Adjusted R-squared: 0.5122
F-statistic: 56.64 on 1 and 52 DF, p-value: 7.187e-10
修正后的回归方程：Y = 55.5658 + 0.5963x
数据分析咨询请扫描二维码
