R语言之纵向数据分析：多级增长模

上一次，我们讨论了如何对长型数据转换成长型的数据，同时还是用了一个随机创建的对照实验数据集来对其增长趋势进行可视化。但是，我们是否能够进一步的分析并预测结果的增长趋势与时间之间的关系。
是的，当然可以！我们可以使用多级增长模型（也称之为层次模型或者混合模型）进行估计。

产生一个水平数据集并把它转成宽格式
下面，我们先从我之前的一篇文章的实例进行讲解：

1. library(MASS)
3. dat.tx.a<-mvrnorm(n=250,mu=c(30,20,28),
4. Sigma=matrix(c(25.0,17.5,12.3,
5. 17.5,25.0,17.5,
6. 12.3,17.5,25.0),nrow=3,byrow=TRUE))
8. dat.tx.b<-mvrnorm(n=250,mu=c(30,20,22),
9. Sigma=matrix(c(25.0,17.5,12.3,
10. 17.5,25.0,17.5,
11. 12.3,17.5,25.0),nrow=3,byrow=TRUE))
13. dat<-data.frame(rbind(dat.tx.a,dat.tx.b))
14. names(dat)<-c('measure.1','measure.2','measure.3')
16. dat<-data.frame(subject.id=factor(1:500),tx=rep(c('A','B'),each=250),dat)
18. rm(dat.tx.a,dat.tx.b)
20. dat<-reshape(dat,varying=c('measure.1','measure.2','measure.3'),
21. idvar='subject.id',direction='long')

多级增长模型

这里有很多R语言包可以帮助你进行多级分析，其中，我发现lme4包是最好的一个，因为它使用比较简单，而且建模能力也很强（尤其是输出二进制结果或者计数结果）。当然，nlme包也是相当不错的，它可以给连续型结果提供了类似的结果（正态/高斯分布）。

1. install.packages('lme4')
2. library(lme4)
3. m<-lmer(measure~time+(1|subject.id),data=dat)

如果你之前做过回归分析，你应该对这样的语法结构比较熟悉了。通常来说，它就是lm()函数当中含有额外的随即效应公式。
随即效应，如果你对这个术语不熟悉的话，其实可以这么理解，通常来说，它就是一个实验所无法控制的误差，即变化。因此，比方来说，一个志愿者所收到的治疗效果就是一种混合的效应，因为，假设我们是实验人员，我们会决定哪些人接受A治疗方案，哪些接受B治疗方案。然而，抑郁症评分的基线在治疗的初始阶段会因人而异，一些人可能会更加抑郁，一些其实并没有这么忧郁。由于这是无法控制的，我们会把它看成是随即效应。
尤其是，抑郁评分基线的差异可以看作是一个随机区间（即，不同的志愿者参与不同等级的治疗）。我们也可以在建模的时候，对它们的斜率进行随机设置：例如，如果我们有理由相信尽管大家接受的治疗是一样的，一些参与治疗的人可以收到很好的疗效，而其它人则收效甚微。
结果的随机效应部分陈述了数据的方差结构。在这个模型中，存在两种方差结构：残差（通常用在线性模型）和个体之间的差异（即，每一个主体的id）。量化个体差异程度的一种常用方法就是研究同类相关系数（ICC）。我们可能可以从多级模型那里计算ICC，而且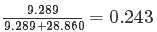,这意味着，24.3%的抑郁平分变化可以由个体差异程度来解释。
现在，我们把目光转到修正效应。嗯…，那些p值在哪里呢？这，尽管SAS和其它统计软件有给多级模型的修正效应计算提供p值方面的信息，其实，很多统计学家的计算结果并不一致。举个简单的例子，我们对自由度与这些t检验的关联程度了解的不深，而且没有自由度的话，我们比不知道t检验的具体分布，因此，我们无法得到p值方面的信息。SAS和其它软件都有相应的工作区来处理估计值，这时lme4包开发人员感到不舒服的地方。结果，lmer包并没有刻意的汇报p值的信息（所以，不要害怕你得不到p值！或许有其它的方法在显著性的测量上比我们的模型做的还好）。
这么说，如果你绝对需要p值，我们可以使用基于lme4包所产生的lmerTest包来估算p值。

含有p估计值的多级增长模型

下面大部分的代码和上面的类似，除非我们要使用lmerTest包。

1. # install.packages('lme4')
2. # Please note the explanation and limitations:
3. # https://stat.ethz.ch/pipermail/r-help/2006-May/094765.html
4. library(lmerTest)
5. m<-lmer(measure~time+(1|subject.id),data=dat)

其结果很相似，但现在，我们可以得到自由度和p的估计值。所以，我们可以很自信的说普通RCT参与治疗的人，现在，随着时间的推移，他们的抑郁症得分在下降，其速度为每下降1分，下降的量为2.24。

1. summary(m)
2. Linearmixed model fitbyREML t-tests
3. useSatterthwaiteapproximations to
4. degrees of freedom[merModLmerTest]
5. Formula:measure~time+(1|subject.id)
6. Data:dat
8. REML criterion at convergence:9639.6
10. Scaledresiduals:
11. Min1QMedian3QMax
12. -2.45027-0.705960.008320.659512.78759
14. Randomeffects:
15. GroupsNameVarianceStd.Dev.
16. subject.id(Intercept)9.2893.048
17. Residual28.8605.372
18. Numberof obs:1500,groups:subject.id,500
20. Fixedeffects:
21. EstimateStd.Errordf t valuePr(>|t|)
22. (Intercept)29.85080.39151449.400076.25<2e-16***
23. time-2.24200.1699999.0000-13.20<2e-16***
24. ---
25. Signif.codes:0‘***’0.001‘**’0.01‘*’0.05‘.’0.1‘’1
27. CorrelationofFixedEffects:
28. (Intr)
29. time-0.868

计算95%置信区间和预测区间

有时，我们想在单个轨迹的均值进行作图。如果要展示均值里的一些不确定因素，我们需要使用拟合好的模型，利用拟合值进行计算，算出95%置信区间和95%预测区间。

1. # See for details: http://glmm.wikidot.com/faq
2. dat.new<-data.frame(time=1:3)
3. dat.new$measure<-predict(m,dat.new,re.form=NA)
5. m.mat<-model.matrix(terms(m),dat.new)
7. dat.new$var<-diag(m.mat%*%vcov(m)%*%t(m.mat))+VarCorr(m)$subject.id[1]
8. dat.new$pvar<-dat.new$var+sigma(m)^2
9. dat.new$ci.lb<-with(dat.new,measure-1.96*sqrt(var))
10. dat.new$ci.ub<-with(dat.new,measure+1.96*sqrt(var))
11. dat.new$pi.lb<-with(dat.new,measure-1.96*sqrt(pvar))
12. dat.new$pi.ub<-with(dat.new,measure+1.96*sqrt(pvar))

第一行代码指出我们想要求出均值的一个点，它们一般来说是在我们这个案例的前三次预测的时候。第二行代码使用了predict()函数来得到模型的均值，它不考虑条件随机效应（re.form=NA)。第三第四行计算了均值的方差，一般来说是矩阵交叉与随机效应截距相加。第五行计算了单个观测值的方差，它的方差等于方差均值假设残差方差。第六到第九行则按普通方法，并假设它是正态分布来计算95%置信区间和预测区间。最后所给的代码是：

1. dat.new
2. time measurevarpvar ci.lb ci.ub pi.lb pi.ub
3. 127.7242110.8566943.0405421.2661134.1823114.86557440.58285
4. 225.2234210.8245143.0083518.7749031.6719412.36959238.07725
5. 322.7226310.8566943.0405416.2645329.180739.86399335.58127

作均值图像

最后，我们要作它的95%置信区间和95%预测区间的图像了。注意，预测区间的图像要宽于置信区间。也就是说，预测均值的结果比用单个值预测要好。

1. ggplot(data=dat.new,aes(x=time,y=measure))+
2. geom_line(data=dat,alpha=.02,aes(group=subject.id))+
3. geom_errorbar(width=.02,colour='red',
4. aes(x=time-.02,ymax=ci.ub,ymin=ci.lb))+
5. geom_line(colour='red',linetype='dashed',aes(x=time-.02))+
6. geom_point(size=3.5,colour='red',fill='white',aes(x=time-.02))+
7. geom_errorbar(width=.02,colour='blue',
8. aes(x=time+.02,ymax=pi.ub,ymin=pi.lb))+
9. geom_line(colour='blue',linetype='dashed',aes(x=time+.02))+
10. geom_point(size=3.5,colour='blue',fill='white',aes(x=time+.02))+
11. theme_bw()

如果你和我一样，对数据也很敏感，你应该能观察到图线的拟合效果并不太好。这里，有两种办法可以得到更好的结果，而这个我们在后面将会讲到。保持关注。