简单易学的机器学习算法—线性支持向量机

一、线性支持向量机的概念

    线性支持向量机是针对线性不可分的数据集的，这样的数据集可以通过近似可分的方法实现分类。对于这样的数据集，类似线性可分支持向量机，通过求解对应的凸二次规划问题，也同样求得分离超平面
以及相应的分类决策函数
二、与线性可分支持向量机的比较
    线性支持向量机与线性可分支持向量机最大的不同就是在处理的问题上，线性可分支持向量机处理的是严格线性可分的数据集，而线性支持向量机处理的是线性不可分的数据集，然而，在基本的原理上他们却有着想通之处。这里的线性不可分是指数据集中存在某些点不能满足线性可分支持向量机的约束条件：。
    具体来讲，对于特征空间上的训练数据集，且不是线性可分的，即存在某些特异点不满足的约束条件，若将这些特异点去除，那么剩下的数据点是线性可分的，由此可见，线性可分支持向量机是线性支持向量机的特殊情况。为了解决这样的问题，对每个样本点引入一个松弛变量，且，则上述的约束条件被放宽，即：

此时目标函数变为：
其中称为惩罚参数，且。在线性支持向量机中加入了惩罚项，与线性可分支持向量的应间隔最大化相对应，在线性支持向量机中称为软间隔最大化。数据分析师培训
三、线性支持向量机的原理
    由上所述，我们得到线性支持向量机的原始问题：

接下来的问题就变成如何求解这样一个最优化问题(称为原始问题)。引入拉格朗日函数：

其中，。
    此时，原始问题即变成
利用拉格朗日函数的对偶性，将问题变成一个极大极小优化问题：

    首先求解，将拉格朗日函数分别对求偏导，并令其为0：

即为：
将其带入拉格朗日函数，即得：

    第二步，求，即求：

由可得，因为在第二步求极大值的过程中，函数只与a有关。
    将上述的极大值为题转化为极小值问题：

这就是原始问题的对偶问题。
四、线性支持向量机的过程
1、设置惩罚参数，并求解对偶问题：

假设求得的最优解为；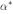
2、计算原始问题的最优解：
选择中满足的分量，计算：

3、求分离超平面和分类决策函数：
分离超平面为：
分类决策函数为：
五、实验的仿真
1、解决线性可分问题
    与博文“简单易学的机器学习算法——线性可分支持向量机”实验一样，其中取中的最大值。
MATLAB代码为
[plain] view plain copy 在CODE上查看代码片派生到我的代码片
%% 线性支持向量机  
 
% 清空内存  
clear all;  
clc;  
 
%简单的测试数据集  
X = [3,3;4,3;1,1];  
y = [1,1,-1];%标签  
A = [X,y'];  
 
m = size(A);%得到训练数据的大小  
 
 
% 区分开特征与标签  
X = A(:,1:2);  
Y = A(:,m(1,2))';  
 
for i = 1:m(1,1)  
    X(i,:) = X(i,:)*Y(1,i);  
end  
 
 
 
%% 对偶问题，用二次规划来求解  
H = X*X';  
 
f = ones(m(1,1),1)*(-1);  
B = Y;  
b = 0;  
lb = zeros(m(1,1),1);  
% 调用二次规划的函数  
[x,fval,exitflag,output,lambda] = quadprog(H,f,[],[],B,b,lb);  
 
% 定义C  
C = max(x);  
 
% 求原问题的解  
n = size(x);  
w = x' * X;  
 
k = 1;  
for i = 1:n(1,1)  
    if x(i,1) > 0 && x(i,1)<C  
        b(k,1) = Y(1,i)-w*X(i,:)'*Y(1,i);  
        k = k +1;  
    end  
end  
b = mean(b);  
 
% 求出分离超平面  
 
y_1 = [0,4];  
for i = 1:2  
    y_2(1,i) = (-b-w(1,1)*y_1(1,i))./w(1,2);  
end  
 
hold on  
plot(y_1,y_2);  
for i = 1:m(1,1)  
    if A(i,m(1,2)) == -1  
        plot(A(i,1),A(i,2),'og');  
    elseif A(i,m(1,2)) == 1  
        plot(A(i,1),A(i,2),'+r')  
    end  
end  
axis([0,7,0,7])    
hold off  

实验结果为：

(线性可分问题的分离超平面)
2、解决线性不可分问题
问题为：

(线性不可分问题)

MATLAB代码：
[plain] view plain copy 在CODE上查看代码片派生到我的代码片
%% 线性支持向量机  
 
% 清空内存  
clear all;  
clc;  
 
% 导入测试数据  
A = load('testSet.txt');  
 
% 处理数据的标签  
m = size(A);%得到训练数据的大小  
for i = 1:m(1,1)  
    A(i,m(1,2)) = A(i,m(1,2))*2-1;  
end  
 
 
 
% 区分开特征与标签  
X = A(:,1:2);  
Y = A(:,m(1,2))';  
 
for i = 1:m(1,1)  
    X(i,:) = X(i,:)*Y(1,i);  
end  
 
 
 
%% 对偶问题，用二次规划来求解  
H = X*X';  
 
f = ones(m(1,1),1)*(-1);  
B = Y;  
b = 0;  
lb = zeros(m(1,1),1);  
% 调用二次规划的函数  
[x,fval,exitflag,output,lambda] = quadprog(H,f,[],[],B,b,lb);  
 
% 定义C  
% C = mean(x);  
C = max(x);  
 
% 求原问题的解  
n = size(x);  
w = x' * X;  
 
k = 1;  
for i = 1:n(1,1)  
    if x(i,1) > 0 && x(i,1)<C  
        b(k,1) = Y(1,i)-w*X(i,:)'*Y(1,i);  
        k = k +1;  
    end  
end  
b = mean(b);  
 
% 求出分离超平面  
 
y_1 = [-4,4];  
for i = 1:2  
    y_2(1,i) = (-b-w(1,1)*y_1(1,i))./w(1,2);  
end  
 
hold on  
plot(y_1,y_2);  
for i = 1:m(1,1)  
    if A(i,m(1,2)) == -1  
        plot(A(i,1),A(i,2),'og');  
    elseif A(i,m(1,2)) == 1  
        plot(A(i,1),A(i,2),'+r')  
    end  
end  
hold off  

实验结果为：

(线性不可分问题的分离超平面)
注：这里的的取值很重要，的取值将决定分类结果的准确性。