 京公网安备 11010802034615号
经营许可证编号:京B2-20210330
京公网安备 11010802034615号
经营许可证编号:京B2-20210330
单样本t检验的spss实现

直接来看一个例子:
常规种植条件下某玉米品的平均穗重为 300g 。现在采用根外施肥(即将肥料制成液体养分,喷洒到玉米的叶面)后,调查了 20 个玉米棒 ,其穗重如表 1所示。问:改用叶面施肥后,穗重是 否显著增加了 ?(置信度为 95% 或者显著水平 α=0.05)

表1 20个玉米穗的重量(单位:g)
这是一个单尾测验,原假设和备择假设是:

原假设(无效假设):叶面施肥没有增产效果。
备择假设 :叶面施肥有增产效果
在SPSS中不能直接进行单尾测验,但是SPSS却可以输出t统计量的双侧检验相伴概率sig,将得到的相伴概率除以2,即得到单尾测验的相伴概率。将这个相伴概率与0.05进行比较,小于0.05则拒绝原假设。
单样本t检验的SPSS操作
首先将数据导入或者录入到spss中,然后依次 选择分析 <均值比较 <单样本t检验. 出现如下图所示的窗口。

将要检验的变量“穗重”选入到“检验变量”窗口,同时输入给定的用于对比的那个值,此处为常规种植条件下的穗重均值300.设置完毕后,点击确定。输出结果中的描述性统计这里就不讨论了,直接看t检验的结果。

你可以找一本统计学教材,对着t分布表,查看一下自由度为19,显著水平为0.05时,的双侧检验的t临界值,将这里得到的t值与那个临界值进行比较,如果这里的t值大于那个临界值,则拒绝原假设,这和p值小于0.05是等价的。
如下图所示,这里得到的双侧t检验相伴概率为0.006,那么单侧相伴概率为0.003,无论是双侧检验还是单侧检验,都可以拒绝原假设,考虑到叶面施肥后的穗重均值为300+7=307,因此认为叶面施肥能够极显著地增加穗重。
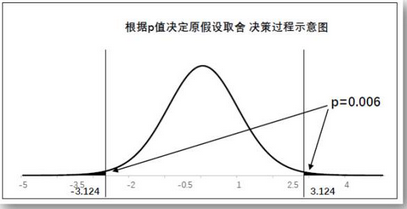
双侧检验与单侧检验
下面两张图片中,第一个图中黑色区域表示的是单侧检验的拒绝域。第二个图表示的双侧检验的拒绝域。同样是0.05的置信水平,双侧检验与单侧检验,临界值是不同的,因为黑色区域的位置不同,尽管它们的总面积是相等的。

进行大端单尾测验时,当计算得到的t统计量大于黑色区域与白色区域的临界位置对应的横轴值时,拒绝原假设。而这时,相伴概率也一定小于0.05,因此使用相伴概率和t临界值来决定原假设的取舍,原理本质上是一样的。只不过教材上进行案例讲解时,一般使用临界值,因为相伴概率计算困难。而统计软件一般直接给出相伴概率。(相伴概率即为p值或者spss输出的sig值。)

进行双侧检验时,计算得到的统计量落入两边任意一块黑色区域,就应该拒绝原假设。或者相伴概率小于0.05时,拒绝原假设。(黑色区域表示的是一个很小的概率,这样小的概率,通过一次试验一般是不会发生,如果发生,说明原假设有问题,说明真实的分布不是原假设成立时的这个分布,均值要改变才行,均值改变了才能符合被检验的数据,所以被检验的数据的均值与原来那个设定值是不同的。)
单侧检验的R语言实现
如果你一定要直接得出单侧检验的结果,那也不是没有办法,R语言可以直接得出单侧检验的结果。给出代码如下:
t_test01.1<-read.csv(file="D:/单样本t检验_玉米.csv",header=TRUE)
#载入数据
t.test(t_test01.1$穗重,
alternative =c("greater"),
mu =300, paired =FALSE,
conf.level =0.95
) #进行单样本t检验
输出结果如下
OneSample t-test
data: t_test01.1$穗重
t=3.1239, df=19, p-value =0.002794
alternative hypothesis: true mean is greater than 300
95 percent confidence interval:
303.1254 Inf
sample estimates:
mean of x
307
得到 p-value =0.002794<0.05,拒绝原假设,选择备择假设:alternative hypothesis: true mean is greater than 300。(实际均值大于300)

数据分析咨询请扫描二维码
若不方便扫码,搜微信号:CDAshujufenxi
在金融行业的数字化转型进程中,SQL作为数据处理与分析的核心工具,贯穿于零售银行、证券交易、保险理赔、支付结算等全业务链条 ...
2025-12-24在数据分析领域,假设检验是验证“数据差异是否显著”的核心工具,而独立样本t检验与卡方检验则是其中最常用的两种方法。很多初 ...
2025-12-24在企业数字化转型的深水区,数据已成为核心生产要素,而“让数据可用、好用”则是挖掘数据价值的前提。对CDA(Certified Data An ...
2025-12-24数据分析师认证考试全面升级后,除了考试场次和报名时间,小伙伴们最关心的就是报名费了,报 ...
2025-12-23CDA中国官网是全国统一的数据分析师认证报名网站,由认证考试委员会与持证人会员、企业会员以及行业知名第三方机构共同合作,致 ...
2025-12-23在Power BI数据可视化分析中,矩阵是多维度数据汇总的核心工具,而“动态计算平均值”则是矩阵分析的高频需求——无论是按类别计 ...
2025-12-23在SQL数据分析场景中,“日期转期间”是高频核心需求——无论是按日、周、月、季度还是年度统计数据,都需要将原始的日期/时间字 ...
2025-12-23在数据驱动决策的浪潮中,CDA(Certified Data Analyst)数据分析师的核心价值,早已超越“整理数据、输出报表”的基础层面,转 ...
2025-12-23在使用Excel数据透视表进行数据分析时,我们常需要在透视表旁添加备注列,用于标注数据背景、异常说明、业务解读等关键信息。但 ...
2025-12-22在MySQL数据库的性能优化体系中,索引是提升查询效率的“核心武器”——一个合理的索引能将百万级数据的查询耗时从秒级压缩至毫 ...
2025-12-22在数据量爆炸式增长的数字化时代,企业数据呈现“来源杂、格式多、价值不均”的特点,不少CDA(Certified Data Analyst)数据分 ...
2025-12-22在企业数据化运营体系中,同比、环比分析是洞察业务趋势、评估运营效果的核心手段。同比(与上年同期对比)可消除季节性波动影响 ...
2025-12-19在数字化时代,用户已成为企业竞争的核心资产,而“理解用户”则是激活这一资产的关键。用户行为分析系统(User Behavior Analys ...
2025-12-19在数字化转型的深水区,企业对数据价值的挖掘不再局限于零散的分析项目,而是转向“体系化运营”——数据治理体系作为保障数据全 ...
2025-12-19在数据科学的工具箱中,析因分析(Factor Analysis, FA)、聚类分析(Clustering Analysis)与主成分分析(Principal Component ...
2025-12-18自2017年《Attention Is All You Need》一文问世以来,Transformer模型凭借自注意力机制的强大建模能力,在NLP、CV、语音等领域 ...
2025-12-18在CDA(Certified Data Analyst)数据分析师的时间序列分析工作中,常面临这样的困惑:某电商平台月度销售额增长20%,但增长是来 ...
2025-12-18在机器学习实践中,“超小数据集”(通常指样本量从几十到几百,远小于模型参数规模)是绕不开的场景——医疗领域的罕见病数据、 ...
2025-12-17数据仓库作为企业决策分析的“数据中枢”,其价值完全依赖于数据质量——若输入的是缺失、重复、不一致的“脏数据”,后续的建模 ...
2025-12-17在CDA(Certified Data Analyst)数据分析师的日常工作中,“随时间变化的数据”无处不在——零售企业的每日销售额、互联网平台 ...
2025-12-17