机器学习中的概率问题

机器学习的过程可以理解为计算机通过分析大量的数据获得模型，并通过获得的模型进行预测的过程。机器学习的模型可以有多种表示，例如线性回归模型，SVM模型，决策树模型，贝叶斯模型。

概率类型

在理解概率模型之前，首先要理解的各种概率类型所表示的确切含义。

1.先验概率

某事件发生的概率。

2.条件概率

在某种条件下，事件A发生的概率，可以是基于历史数据的统计，可以由背景常识得出，也可以是人的主观观点给出。一般都是单独事件概率，如P(x),P(y)。

3.后验概率

条件概率的一种特殊情况，它限定了事件为隐变量取值(不可观测)，而条件为观测结果。

4.联合概率

表示多个事件同时发生的概率。

5.似然概率

条件概率的一种，针对参数而言，意思是某参数(某事件发生的概率)取得某一值得概率。

正向过程（普通概率）：给定参数后，预测即将发生的事件的可能性，以投掷硬币为例，已知一枚均匀硬币，投掷出正反面的概率均为0.5(给出的参数)，求投掷两次硬币都朝上的概率。

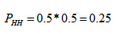
逆向过程（似然概率）：给定事件发生的可能性，求解参数为某一值得可能性，以投掷硬币为例，已知一枚均匀硬币，投掷两次都是正面朝上(条件)，求正面朝上的概率为0.5的可能性是多少。

求正面朝上概率为x的似然：

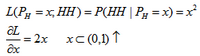
通过计算不同的正面朝上的概率的可能性，可以得到一条似然函数曲线：

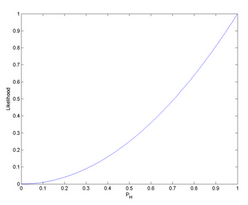
似然函数曲线

最大似然概率，最大似然概率，在已知观测数据的条件下，找到使似然概率最大的参数值作为真实的参数估计。例如从似然函数曲线中可以得知，当PH=1时，似然函数取得最大值。

预测模型的概率表示

在这里我们假设已有的数据为X，可能出现的结果为Y，每一个可能的结果Y都对应一个给出数据X下的条件概率。

机器学习最终得到的结果是实现该条件的概率的最大化。

决策函数和条件概率

决策函数都是很熟悉了，在线性回归，SVM，神经网络中使用的都是决策函数Y=f(X)，在贝叶斯分类中使用的是条件概率分布P(Y|X)。

条件概率分布模型可表示成决策函数

决策函数中隐含着条件概率

例如在线性回归模型中，通过不断训练是误差平方最小化，而误差平方最小化是根据极大似然假设推导而出的。

所以依据决策函数得到的结果满足极大似然概率，同时满足最大条件概率。

判别式模型和生成式模型

实现上述过程，基于是否对P(x|y)直接操作来区分有两种策略：

判别式模型：由数据直接对P(x|y)或决策函数f(x)进行建模，例如线性回归模型，SVM，决策树等，这些模型都预先制定了模型的格式，所需要的就是通过最优化的方法学到最优参数Θ即可。

生成式模型:这种策略并不直接对P(Y|X)进行建模，而是先对联合概率分布P(X,Y)进行建模，然后依据贝叶斯公式P(Y|X)=P(X,Y)P(X)间接的得到我们所期望的模型P(Y|X)，这种策略最常见的算法就是我们接下来要介绍的贝叶斯分类器算法