R语言与数据分析:主成分分析
作为数据分析师,有很多刚刚接触数据分析师的朋友,还不怎么了解主成分分析,看看这两篇,你就搞懂主成分分析了。
第一篇:主成份分析历史
Pearson于1901年提出,再由Hotelling(1933)加以发展的一种多变量统计方法。通过析取主成分显出最大的个别差异,也用来削减回归分析和聚类分析中变量的数目,可以使用样本协方差矩阵或相关系数矩阵作为出发点进行分析。
通过对原始变量进行线性组合,得到优化的指标:把原先多个指标的计算降维为少量几个经过优化指标的计算(占去绝大部分份额)
基本思想:设法将原先众多具有一定相关性的指标,重新组合为一组新的互相独立的综合指标,并代替原先的指标。
成分的保留:Kaiser主张(1960)将特征值小于1的成分放弃,只保留特征值大于1的成分。
接下来以小学生基本生理属性为案例分享下R语言的具体实现,分别选取身高(x1)、体重(x2)、胸围(x3)和坐高(x4)。具体如下:
student<- data.frame( x1=c(148,139,160,149,159,142,153,150,151), x2=c(41 ,34 , 49 ,36 ,45 ,31 ,43 ,43,
42), x3=c(72 ,71 , 77 ,67 ,80 ,66 ,76 ,77,77), x4=c(78 ,76 , 86 ,79 ,86 ,76 ,83 ,79 ,80)
) student.pr <- princomp(student,cor=TRUE) summary(student.pr,loadings=TRUE) screeplot(student.pr,type="
lines")
结果如截图:
 由上图可见四项指标做分析后,给出了4个成分,他们的重要性分别为:0.887932、0.08231182、0.02393843、0.005817781,累积贡献为:0.887932、0.97024379、
由上图可见四项指标做分析后,给出了4个成分,他们的重要性分别为:0.887932、0.08231182、0.02393843、0.005817781,累积贡献为:0.887932、0.97024379、
0.99418222 1.000000000各个成分的碎石图也如上,可见成份1和成份2的累积贡献已经达到95%,因此采用这两个成份便可充分解释学生的基本信息。
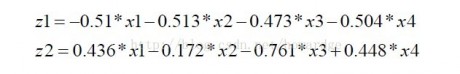 我们可以通过R自动算出各主成份的值,并画出散点图:
我们可以通过R自动算出各主成份的值,并画出散点图:
temp<-predict(student.pr)
plot(temp[,1:2])
结果如图:
观察如图可见两个成分的分离度很高,比较理想。
第二篇: 主成分分析(principal component analysis,PCA)是一种降维技术,把多个变量化为能够反映原始变量大部分信息的少数几个主成分。
设X有p个变量,为n*p阶矩阵,即n个样本的p维向量。首先"数据分析师"对X的p个变量寻找正规化线性组合,使它的方差达到最大,这个新的变量称为第一主成分,抽取第一主成分后,第二主成分的抽取方法与第一主成分一样,依次类推,直到各主成分累积方差达到总方差的一定比例。
主成分分析的计算步骤:
假设样本观测数据矩阵为:
X=(x1,x2,x3,…xp),xi为n个样本在第i个属性上的观测值,是一个列向量
1.对原始数据标准化处理(0均值化处理)
2.计算样本相关系数矩阵
3.计算协方差矩阵的特征值和特征向量
4、选择重要的主成分,并写出主成分表达式
5.计算主成分得分
6.根据主成分得分的数据,做进一步的统计分析。
主成分分析可以得到p个主成分,但是,由于各个主成分的方差是递减的,包含的信息量也是递减的,所以实际分析时,一般不是选取p个主成分,而是根据各个主成分累计贡献率的大小选取前k个主成分,这里贡献率就是指某个主成分的方差占全部方差的比重,实际也就是某个特征值占全部特征值总和的比重。贡献率越大,说明该主成分所包含的原始变量的信息越强。主成分个数k的选取,主要根据主成分的累积贡献率来决定,即一般要求累计贡献率达到85%以上,这样才能保证综合变量能包括原始变量的绝大多数信息。
另外,数据分析师在实际应用中,选择了重要的主成分后,还要注意主成分实际含义解释。主成分分析中一个很关键的问题是如何给主成分赋予新的意义,给出合理的解释。一般而言,这个解释"数据分析师"是根据主成分表达式的系数结合定性分析来进行的。主成分是原来变量的线性组合,在这个线性组合中个变量的系数有大有小,有正有负,有的大小相当,因而不能简单地认为这个主成分是某个原变量的属性的作用,线性组合中各变量系数的绝对值大者表明该主成分主要综合了绝对值大的变量,有几个变量系数大小相当时,应认为这一主成分是这几个变量的总和,这几个变量综合在一起应赋予怎样的实际意义,这要结合具体实际问题和专业,给出恰当的解释,进而才能达到深刻分析的目的 。
在R里手工统计过程如下:
> #数据集
> y=USArrests
> #相关矩阵
> c=cor(y)
> #特征值
> e=eigen(c)
> e
$values #特征值
[1] 2.4802416 0.9897652 0.3565632 0.1734301
$vectors 特征向量,也就是主成分的表达式
[,1] [,2] [,3] [,4]
[1,] -0.5358995 0.4181809 -0.3412327 0.64922780
[2,] -0.5831836 0.1879856 -0.2681484 -0.74340748
[3,] -0.2781909 -0.8728062 -0.3780158 0.13387773
[4,] -0.5434321 -0.1673186 0.8177779 0.08902432
> # 计算标准化的主成分得分
> scale( as.matrix(y))%*%e$vector
[,1] [,2] [,3] [,4]
Alabama -0.97566045 1.12200121 -0.43980366 0.154696581
Alaska -1.93053788 1.06242692 2.01950027 -0.434175454
Arizona -1.74544285 -0.73845954 0.05423025 -0.826264240
Arkansas 0.13999894 1.10854226 0.11342217 -0.180973554
…..
West Virginia 2.08739306 1.41052627 0.10372163 0.130583080
Wisconsin 2.05881199 -0.60512507 -0.13746933 0.182253407
Wyoming 0.62310061 0.31778662 -0.23824049 -0.164976866
R中下面两个函数可以用做主成分分析
princomp(x, cor = FALSE, scores = TRUE, covmat = NULL,
subset = rep(TRUE, nrow(as.matrix(x))), …)
cor =TRUE 是使用相关矩阵求主成分,否则使用协方差矩阵。
prcomp(x, retx = TRUE, center = TRUE, scale. = FALSE,
tol = NULL, …)
scale =TRUE 即使用相关矩阵求主成分夬否则使用协方差矩阵
求主成分。
> # prcomp() 的用法
> p=prcomp(USArrests, scale=T)
> p
Standard deviations:
[1] 1.5748783 0.9948694 0.5971291 0.4164494
Rotation:
PC1 PC2 PC3 PC4
Murder -0.5358995 0.4181809 -0.3412327 0.64922780
Assault -0.5831836 0.1879856 -0.2681484 -0.74340748
UrbanPop -0.2781909 -0.8728062 -0.3780158 0.13387773
Rape -0.5434321 -0.1673186 0.8177779 0.08902432
> summary(p)
Importance of components:
PC1 PC2 PC3 PC4
Standard deviation 1.5749 0.9949 0.59713 0.41645
Proportion of Variance 0.6201 0.2474 0.08914 0.04336
Cumulative Proportion 0.6201 0.8675 0.95664 1.00000
#计算标准化的主成分得分
> predict(p)cda数据分析师培训
结果和手工统计的一样。

数据分析咨询请扫描二维码
若不方便扫码,搜微信号:CDAshujufenxi
CDA持证人简介:居瑜 ,CDA一级持证人,国企财务经理,13年财务管理运营经验,在数据分析实践方面积累了丰富的行业经验。 一、 ...
2025-04-16持证人简介: CDA持证人刘凌峰,CDA L1持证人,微软认证讲师(MCT)金山办公最有价值专家(KVP),工信部高级项目管理师,拥有 ...
2025-04-15持证人简介:CDA持证人黄葛英,ICF国际教练联盟认证教练,前字节跳动销售主管,拥有丰富的行业经验。在实际生活中,我们可能会 ...
2025-04-14在 Python 编程学习与实践中,Anaconda 是一款极为重要的工具。它作为一个开源的 Python 发行版本,集成了众多常用的科学计算库 ...
2025-04-14随着大数据时代的深入发展,数据运营成为企业不可或缺的岗位之一。这个职位的核心是通过收集、整理和分析数据,帮助企业做出科 ...
2025-04-11持证人简介:CDA持证人黄葛英,ICF国际教练联盟认证教练,前字节跳动销售主管,拥有丰富的行业经验。 本次分享我将以教培行业为 ...
2025-04-11近日《2025中国城市长租市场发展蓝皮书》(下称《蓝皮书》)正式发布。《蓝皮书》指出,当前我国城市住房正经历从“增量扩张”向 ...
2025-04-10在数字化时代的浪潮中,数据已经成为企业决策和运营的核心。每一位客户,每一次交易,都承载着丰富的信息和价值。 如何在海量客 ...
2025-04-09数据是数字化的基础。随着工业4.0的推进,企业生产运作过程中的在线数据变得更加丰富;而互联网、新零售等C端应用的丰富多彩,产 ...
2025-04-094月7日,美国关税政策对全球金融市场的冲击仍在肆虐,周一亚市早盘,美股股指、原油期货、加密货币、贵金属等资产齐齐重挫,市场 ...
2025-04-08背景 3月26日,科技圈迎来一则重磅消息,苹果公司宣布向浙江大学捐赠 3000 万元人民币,用于支持编程教育。 这一举措并非偶然, ...
2025-04-07在当今数据驱动的时代,数据分析能力备受青睐,数据分析能力频繁出现在岗位需求的描述中,不分岗位的任职要求中,会特意标出“熟 ...
2025-04-03在当今数字化时代,数据分析师的重要性与日俱增。但许多人在踏上这条职业道路时,往往充满疑惑: 如何成为一名数据分析师?成为 ...
2025-04-02最近我发现一个绝招,用DeepSeek AI处理Excel数据简直太爽了!处理速度嘎嘎快! 平常一整天的表格处理工作,现在只要三步就能搞 ...
2025-04-01你是否被统计学复杂的理论和晦涩的公式劝退过?别担心,“山有木兮:统计学极简入门(Python)” 将为你一一化解这些难题。课程 ...
2025-03-31在电商、零售、甚至内容付费业务中,你真的了解你的客户吗? 有些客户下了一两次单就消失了,有些人每个月都回购,有些人曾经是 ...
2025-03-31在数字化浪潮中,数据驱动决策已成为企业发展的核心竞争力,数据分析人才的需求持续飙升。世界经济论坛发布的《未来就业报告》, ...
2025-03-28你有没有遇到过这样的情况?流量进来了,转化率却不高,辛辛苦苦拉来的用户,最后大部分都悄无声息地离开了,这时候漏斗分析就非 ...
2025-03-27TensorFlow Datasets(TFDS)是一个用于下载、管理和预处理机器学习数据集的库。它提供了易于使用的API,允许用户从现有集合中 ...
2025-03-26"不谋全局者,不足谋一域。"在数据驱动的商业时代,战略级数据分析能力已成为职场核心竞争力。《CDA二级教材:商业策略数据分析 ...
2025-03-26