使用Excel绘制F分布概率密度函数图表

利用Excel绘制t分布的概率密度函数的相同方式，可以绘制F分布的概率密度函数图表。
　　F分布的概率密度函数如下图所示：
 

 
　　其中：μ为分子自由度，ν为分母自由度
　　Γ为伽马函数的的符号
　　由于Excel没有求F分布的概率密度函数可用，但是F分布中涉及到GAMMALN()函数，而excel是提供GAMMALN()函数的，所以我们可以使用excel中的GAMMALN()函数的运算来计算得到F分布的概率密度函数。（可参见【附录】）
　　经转换后上述公式为：
F(X,df1,df2)=EXP(GAMMALN((DF1+DF2)/2))*(DF1^(DF1/2))*(DF2^(DF2/2))*(X^(DF1/2-1))/EXP(GAMMALN(DF1/2))/EXP(GAMMALN(DF2/2))/((DF2+DF1*X)^((DF1+DF2)/2))
                         ……………………………………………………………公式（1）
　　现以分子自由度μ=20，分母自由度ν=20为例，求F分布的图表，可由以下几步进行：
　　第1步 在Excel单元格中输入自变量
　　在A列中，在单元格A2中输入0，在单元格A3中输入0.1，递增0.1，选中单元格A2与A3，按住右下角的填充控制点一直拖到单元格A46是4.4为止，A列的这些数据就作为随机变量t的取值。
　　第2步 在单元格B2中输入计算t分布的概率密度函数的公式
　　对于公式（1），由于自由度μ=20 ，ν=20则由DF1=20,DF2=20代入；自变量X就是单元格A2的值，所以按Excel相对引用的规则，X由A2代入即可，于是单元格B2内容是
=EXP(GAMMALN((20+20)/2))/(EXP(GAMMALN(20/2))*EXP(GAMMALN(20/2)))*(20/20)^(20/2)*A2^(20/2-1)*(1+20/20*A2)^(-1/2*(20+20))
　　第3步 复制公式
　　按住单元格B2右下角的填充控制点，向下一直拖曳到B46，将B2的公式填充复制到B列的相应的单元格。
　　第4步 作F分布概率密度函数图表
　　选择A1：B46，选“插入”-“图表”-“散点图”-“带平滑线的散点图”，输入标题，调整字号、线型等格式，完成t分布概率密度函数图，如图-1所示：

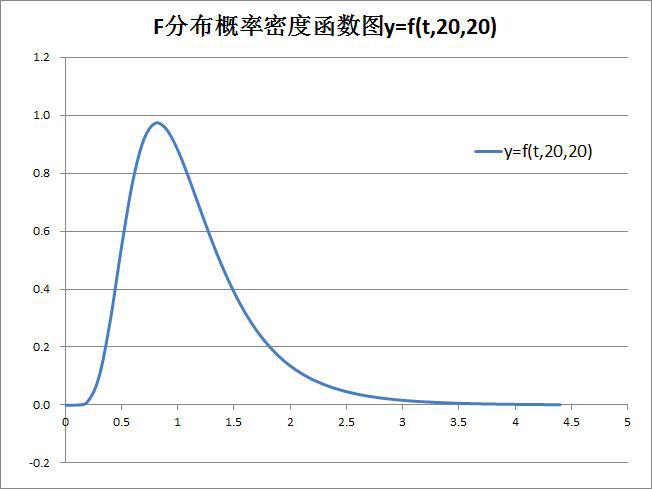
　　如将上图的图表类型换成二维面积图，则如图-2-1(2003版)和图-2-2（2010版）所示：

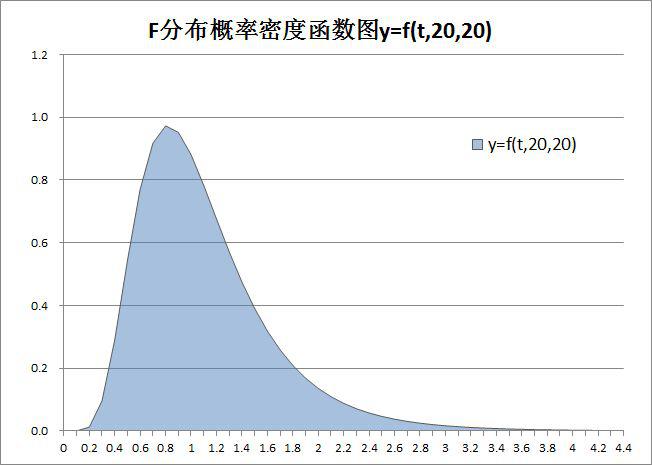
　　如将上图的图表类型换成三维面积图，则如图-3-1（2003版）和图-3-2（2010版）所示：

　　为 了方便调整不同的自由度参数值观察图形变化，在Excel数据表中可在第一行的某几个单元格如I1、I2；J1、J2；K1、K2；L1、L2；M1、 M2输入不同参数，然后在公式引用这几个参数时使用不同的方式：列数据为相对引用，而行数据为绝对引用，如I$1、I$2；J$1、J$2；K$1、 K$2；L$1、L$2；M$1、M$2。而A列自变量值则使用：列数据为绝对引用，而行数据为相对引用，如$A4、$A5、$A6等。  
　　例：B4单元格的公式则为：
=EXP(GAMMALN((I$1+I$2)/2))*(I$1^(I$1/2))*(I$2^(I$2/2))*($A4^(I$1/2-1))/EXP(GAMMALN(I$1/2))/EXP(GAMMALN(I$2/2))/((I$2+I$1*$A4)^((I$1+I$2)/2))
　　这样引用的公式可以直接拖曳复制B4：F48。
　　数据表输入截图如图-4：

    
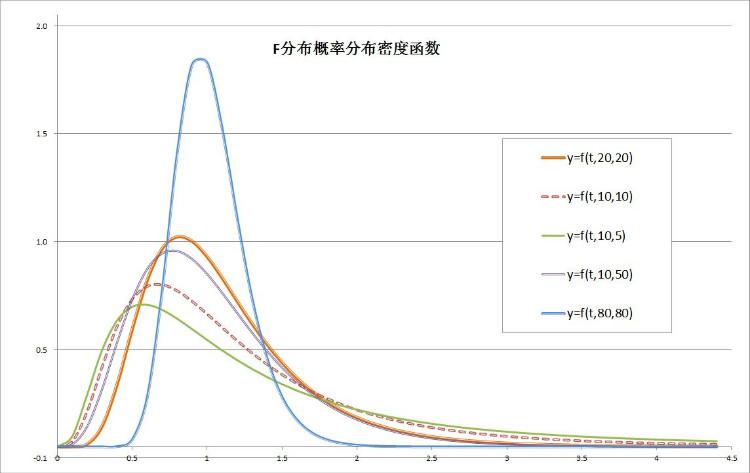
　　在公式输入后，选择单元格区间A3：F48，在同一图表作出五种不同自由度的平滑曲线的散点图，如图-5所示： 

　　【附录：关于GAMMALN（）函数和EXP（）函数】
　　函数 GAMMALN 的计算公式如下： 
 

 
　　伽马函数Γ（x）是个定积分，无法直接计算，可由GAMMALN（）函数和EXP（）函数，并利用对数恒等式：
 

 
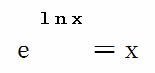
　　间接求得，下面对以上内容使用Excel中的相关文字加以说明。
 GAMMALN函数的作用： 返回伽玛函数Γ(x)的自然对数。 
 　　语法： 
　　GAMMALN(x)
　　 X为需要计算函数 GAMMALN 的数值。
　　 GAMMALN(x)=LN(Γ（x）)
　　说明： 
　　如果 x 为非数值型，函数 GAMMALN 返回错误值 #VALUE!。 
　　如果 x ≤ 0，函数 GAMMAIN 返回错误值 #NUM!。 
　　数字 e 的 GAMMALN(i) 次幂等于 (i-1)!，其中 i 为整数,常数 e 等于 2.71828182845904，是自然对数的底数。 
　　GAMMALN(8)=8.525161
　　EXP(GAMMALN(8))=5040=(8-1)!=FACT(7)
　　FACT(N)为返回N-1的阶乘（N-1）！=1×2×3×4×…×(N-2)×(N-1)的函数（其中N为自然数）
　　关于EXP（）函数：
　　EXP（）返回 e 的 n 次幂。常数 e 等于 2.71828182845904，是自然对数的底数。
　　语法
　　EXP(number)
　　Number 为底数 e 的指数。
　　说明
　　若要计算以其他常数为底的幂，请使用指数操作符 (^)。 
　　EXP 函数是计算自然对数的 LN 函数的反函数。 
　　EXP(1)=2.718282（e的近似值）
　　EXP(2)=7.389056
　　EXP(1)=20.08554
　　EXP(LN(3))=3
　　于是为求伽马函数Γ（x）首先要回忆一个最基本的恒等式：

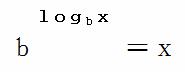
　　即可得：

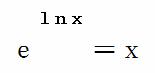
　　把该恒等式用于伽马函数的取得，可以由以下两步进行：
　　先用GAMMALN(x)，取得自然对数；
　　再用EXP(GAMMALN(x)),取得伽马函数的值。