 京公网安备 11010802034615号
经营许可证编号:京B2-20210330
京公网安备 11010802034615号
经营许可证编号:京B2-20210330
python 实例简述 k-近邻算法的基本原理
首先我们一个样本集合,也称为训练样本集,在训练样本集中每个数据都存在一个标签用来指明该数据的所属分类。在输入一个新的未知所属分类的数据后,将新数据的所有特征和样本集中的所有数据计算距离。从样本集中选择与新数据距离最近的 k 个样本,将 k 个样本中出现频次最多的分类作为新数据的分类,通常 k 是小于20的,这也是 k 的出处。
k近邻算法的优点:精度高,对异常值不敏感,无数据输入假定。
k 近邻算法的缺点:时间复杂度和空间复杂度高
数据范围:数值型和标称型
简单的k 近邻算法实现
第一步:使用 python 导入数据
from numpy import *
import operator
'''simple kNN test'''
#get test data
def createDataSet():
group=array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
labels=['A','A','B','B']
return group,labels
作为例子,直接创建数据集和标签,实际应用中往往是从文件中读取数据集和标签。array 是 numpy 提供的一种数据结构,用以存储同样类型的数据,除了常规数据类型外,其元素也可以是列表和元组。这里 group 就是元素数据类型为 list 的数据集。labels 是用列表表示的标签集合。其中 group 和 labels 中的数据元素一一对应,比如数据点[1.0,1.1]标签是 A,数据点[0,0.1]标签是 B。
第二步:实施 kNN 算法
kNN 算法的自然语言描述如下:
1. 计算已知类别数据集中的所有点与未分类点之间的距离。
2. 将数据集中的点按照与未分类点的距离递增排序。
3. 选出数据集中的与未分类点间距离最近的 n 个点。
4. 统计这 n 个点中所属类别出现的频次。
5. 返回这 n 个点中出现频次最高的那个类别。
实现代码:
def classify0(inX,dataSet,labels,k):
dataSetSize=dataSet.shape[0]
diffMat=tile(inX,(dataSetSize,1))-dataSet
sqDiffMat=diffMat**2
sqDistances=sqDiffMat.sum(axis=1)
distances=sqDistances**0.5
sortedDistIndicies=distances.argsort()
classCount={}
for i in range(k):
voteIlabel=labels[sortedDistIndicies[i]]
classCount[voteIlabel]=classCount.get(voteIlabel,0)+1
sortedClassCount=sorted(classCount.iteritems(),key=operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0]
classify0函数中的四个参数含义分别如下:inX 是希望被分类的数据点的属性向量,dataSet 是训练数据集向量,labels 是标签向量,k 是 kNN 算法的参数 k。
接下来来看看本函数的语句都做了那些事。
第一行dataSetSize=dataSet.shape[0],dataSet 是 array 类型,那么dataSet.shape表示 dataSet 的维度矩阵,dataSet.shape[0]表示第二维的长度,dataSet.shape[1]表示第一维的长度。在这里dataSetSize 表示训练数据集中有几条数据。
第二行tile(inX,(dataSetSize,1))函数用以返回一个将 inX 以矩阵形式重复(dataSetSize,1)遍的array,这样产生的矩阵减去训练数据集矩阵就获得了要分类的向量和每一个数据点的属性差,也就是 diffMat。
第三行**在 python 中代表乘方,那么sqDiffMat也就是属性差的乘方矩阵。
第四行array 的 sum 函数若是加入 axis=1的参数就表示要将矩阵中一行的数据相加,这样,sqDistances的每一个数据就代表输入向量和训练数据点的距离的平方了。
第五行不解释,得到了输入向量和训练数据点的距离矩阵。
第六行sortedDistIndicies=distances.argsort(),其中 argsort 函数用以返回排序的索引结果,直接使用 argsort 默认返回第一维的升序排序的索引结果。
然后创建一个字典。
接下来进行 k 次循环,每一次循环中,找到 i 对应的数据的标签,并将其所在字典的值加一,然后对字典进行递减的按 value 的排序。
这样循环完成后,classCount 字典的第一个值就是kNN 算法的返回结果了,也就是出现最多次数的那个标签。
二维的欧式距离公式如下,很简单:
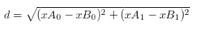
相同的,比如说四维欧式距离公式如下:

第三步:测试分类器
在测试 kNN 算法结果的时候,其实就是讨论分类器性能,至于如何改进分类器性能将在后续学习研究中探讨,现在,用正确率来评估分类器就可以了。完美分类器的正确率为1,最差分类器的正确率为0,由于分类时类别可能有多种,注意在分类大于2时,最差分类器是不能直接转化为完美分类器的。

数据分析咨询请扫描二维码
若不方便扫码,搜微信号:CDAshujufenxi
在企业数据化运营体系中,同比、环比分析是洞察业务趋势、评估运营效果的核心手段。同比(与上年同期对比)可消除季节性波动影响 ...
2025-12-19在数字化时代,用户已成为企业竞争的核心资产,而“理解用户”则是激活这一资产的关键。用户行为分析系统(User Behavior Analys ...
2025-12-19在数字化转型的深水区,企业对数据价值的挖掘不再局限于零散的分析项目,而是转向“体系化运营”——数据治理体系作为保障数据全 ...
2025-12-19在数据科学的工具箱中,析因分析(Factor Analysis, FA)、聚类分析(Clustering Analysis)与主成分分析(Principal Component ...
2025-12-18自2017年《Attention Is All You Need》一文问世以来,Transformer模型凭借自注意力机制的强大建模能力,在NLP、CV、语音等领域 ...
2025-12-18在CDA(Certified Data Analyst)数据分析师的时间序列分析工作中,常面临这样的困惑:某电商平台月度销售额增长20%,但增长是来 ...
2025-12-18在机器学习实践中,“超小数据集”(通常指样本量从几十到几百,远小于模型参数规模)是绕不开的场景——医疗领域的罕见病数据、 ...
2025-12-17数据仓库作为企业决策分析的“数据中枢”,其价值完全依赖于数据质量——若输入的是缺失、重复、不一致的“脏数据”,后续的建模 ...
2025-12-17在CDA(Certified Data Analyst)数据分析师的日常工作中,“随时间变化的数据”无处不在——零售企业的每日销售额、互联网平台 ...
2025-12-17在休闲游戏的运营体系中,次日留存率是当之无愧的“生死线”——它不仅是衡量产品核心吸引力的首个关键指标,更直接决定了后续LT ...
2025-12-16在数字化转型浪潮中,“以用户为中心”已成为企业的核心经营理念,而用户画像则是企业洞察用户、精准决策的“核心工具”。然而, ...
2025-12-16在零售行业从“流量争夺”转向“价值深耕”的演进中,塔吉特百货(Target)以两场标志性实践树立了行业标杆——2000年后的孕妇精 ...
2025-12-15在统计学领域,二项分布与卡方检验是两个高频出现的概念,二者都常用于处理离散数据,因此常被初学者混淆。但本质上,二项分布是 ...
2025-12-15在CDA(Certified Data Analyst)数据分析师的工作链路中,“标签加工”是连接原始数据与业务应用的关键环节。企业积累的用户行 ...
2025-12-15在Python开发中,HTTP请求是与外部服务交互的核心场景——调用第三方API、对接微服务、爬取数据等都离不开它。虽然requests库已 ...
2025-12-12在数据驱动决策中,“数据波动大不大”是高频问题——零售店长关心日销售额是否稳定,工厂管理者关注产品尺寸偏差是否可控,基金 ...
2025-12-12在CDA(Certified Data Analyst)数据分析师的能力矩阵中,数据查询语言(SQL)是贯穿工作全流程的“核心工具”。无论是从数据库 ...
2025-12-12很多小伙伴都在问CDA考试的问题,以下是结合 2025 年最新政策与行业动态更新的 CDA 数据分析师认证考试 Q&A,覆盖考试内容、报考 ...
2025-12-11在Excel数据可视化中,柱形图因直观展示数据差异的优势被广泛使用,而背景色设置绝非简单的“换颜色”——合理的背景色能突出核 ...
2025-12-11在科研实验、商业分析或医学研究中,我们常需要判断“两组数据的差异是真实存在,还是偶然波动”——比如“新降压药的效果是否优 ...
2025-12-11