在进行数据挖掘或者机器学习模型建立的时候,因为在统计学习中,假设数据满足独立同分布,即当前已产生的数据可以对未来的数据进行推测与模拟,因此都是使用历史数据建立模型,即使用已经产生的数据去训练,然后使用该模型去拟合未来的数据。但是一般独立同分布的假设往往不成立,即数据的分布可能会发生变化(distribution
drift),并且可能当前的数据量过少,不足以对整个数据集进行分布估计,因此往往需要防止模型过拟合,提高模型泛化能力。而为了达到该目的的最常见方法便是:正则化,即在对模型的目标函数(objective
function)或代价函数(cost function)加上正则项。
在对模型进行训练时,有可能遇到训练数据不够,即训练数据无法对整个数据的分布进行估计的时候,或者在对模型进行过度训练(overtraining)时,常常会导致模型的过拟合(overfitting)。如下图所示:
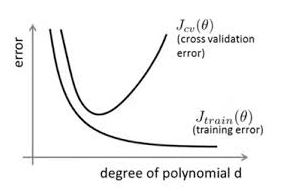
通过上图可以看出,随着模型训练的进行,模型的复杂度会增加,此时模型在训练数据集上的训练误差会逐渐减小,但是在模型的复杂度达到一定程度时,模型在验证集上的误差反而随着模型的复杂度增加而增大。此时便发生了过拟合,即模型的复杂度升高,但是该模型在除训练集之外的数据集上却不work。
方法
提前终止(当验证集上的效果变差的时候)
正则化(Regularization)
L1正则化
L2正则化
数据集扩增(Data augmentation)
Dropout
1、提前终止
对模型进行训练的过程即是对模型的参数进行学习更新的过程,这个参数学习的过程往往会用到一些迭代方法,如梯度下降(Gradient descent)学习算法。Early stopping便是一种迭代次数截断的方法来防止过拟合的方法,即在模型对训练数据集迭代收敛之前停止迭代来防止过拟合。
Early stopping方法的具体做法是,在每一个Epoch结束时(一个Epoch集为对所有的训练数据的一轮遍历)计算validation
data的accuracy,当accuracy不再提高时,就停止训练。这种做法很符合直观感受,因为accurary都不再提高了,在继续训练也是无益的,只会提高训练的时间。那么该做法的一个重点便是怎样才认为validation
accurary不再提高了呢?并不是说validation
accuracy一降下来便认为不再提高了,因为可能经过这个Epoch后,accuracy降低了,但是随后的Epoch又让accuracy又上去了,所以不能根据一两次的连续降低就判断不再提高。一般的做法是,在训练的过程中,记录到目前为止最好的validation accuracy,当连续10次Epoch(或者更多次)没达到最佳accuracy时,则可以认为accuracy不再提高了。此时便可以停止迭代了(Early Stopping)。这种策略也称为“No-improvement-in-n”,n即Epoch的次数,可以根据实际情况取,如10、20、30……
2、数据集扩增
在数据挖掘领域流行着这样的一句话,“有时候往往拥有更多的数据胜过一个好的模型”。因为我们在使用训练数据训练模型,通过这个模型对将来的数据进行拟合,而在这之间又一个假设便是,训练数据与将来的数据是独立同分布的。即使用当前的训练数据来对将来的数据进行估计与模拟,而更多的数据往往估计与模拟地更准确。因此,更多的数据有时候更优秀。但是往往条件有限,如人力物力财力的不足,而不能收集到更多的数据,如在进行分类的任务中,需要对数据进行打标,并且很多情况下都是人工得进行打标,因此一旦需要打标的数据量过多,就会导致效率低下以及可能出错的情况。所以,往往在这时候,需要采取一些计算的方式与策略在已有的数据集上进行手脚,以得到更多的数据。
通俗得讲,数据机扩增即需要得到更多的符合要求的数据,即和已有的数据是独立同分布的,或者近似独立同分布的。一般有以下方法:
从数据源头采集更多数据
复制原有数据并加上随机噪声
重采样
根据当前数据集估计数据分布参数,使用该分布产生更多数据等
如图像处理:
图像平移。这种方法可以使得网络学习到平移不变的特征。
图像旋转。学习旋转不变的特征。有些任务里,目标可能有多种不同的姿态,旋转正好可以弥补样本中姿态较少的问题。
图像镜像。和旋转的功能类似。
图像亮度变化。甚至可以用直方图均衡化。
裁剪。
缩放。
图像模糊。用不同的模板卷积产生模糊图像。
3、正则化
正则化方法是指在进行目标函数或代价函数优化时,在目标函数或代价函数后面加上一个正则项,一般有L1正则与L2正则等。
3.1、L1正则
在原始的代价函数后面加上一个L1正则化项,即所有权重w的绝对值的和,乘以λ/n(这里不像L2正则化项那样,需要再乘以1/2。)
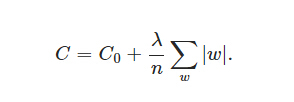
同样先计算导数:
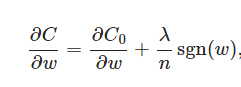
上式中sgn(w)表示w的符号。那么权重w的更新规则为:
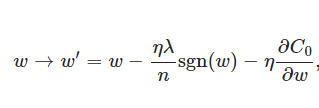
比原始的更新规则多出了η * λ * sgn(w)/n这一项。当w为正时,更新后的w变小。当w为负时,更新后的w变大——因此它的效果就是让w往0靠,使网络中的权重尽可能为0,也就相当于减小了网络复杂度,防止过拟合。
另外,上面没有提到一个问题,当w为0时怎么办?当w等于0时,|W|是不可导的,所以我们只能按照原始的未经正则化的方法去更新w,这就相当于去掉η*λ*sgn(w)/n这一项,所以我们可以规定sgn(0)=0,这样就把w=0的情况也统一进来了。(在编程的时候,令sgn(0)=0,sgn(w>0)=1,sgn(w<0)=-1)
3.2、L2正则化
L2正则化就是在代价函数后面再加上一个正则化项:
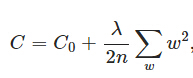
C0代表原始的代价函数,后面那一项就是L2正则化项,它是这样来的:所有参数w的平方的和,除以训练集的样本大小n。λ就是正则项系数,权衡正则项与C0项的比重。另外还有一个系数1/2,1/2经常会看到,主要是为了后面求导的结果方便,后面那一项求导会产生一个2,与1/2相乘刚好凑整。
L2正则化项是怎么避免overfitting的呢?我们推导一下看看,先求导:
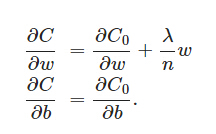
可以发现L2正则化项对b的更新没有影响,但是对于w的更新有影响:

在不使用L2正则化时,求导结果中w前系数为1,现在w前面系数为 1−ηλ/n ,因为η、λ、n都是正的,所以 1−ηλ/n小于1,它的效果是减小w,这也就是权重衰减(weight decay)的由来。当然考虑到后面的导数项,w最终的值可能增大也可能减小。
另外,需要提一下,对于基于mini-batch的随机梯度下降,w和b更新的公式跟上面给出的有点不同:
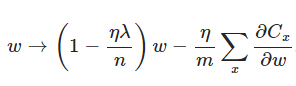

对比上面w的更新公式,可以发现后面那一项变了,变成所有导数加和,乘以η再除以m,m是一个mini-batch中样本的个数。
到目前为止,我们只是解释了L2正则化项有让w“变小”的效果,但是还没解释为什么w“变小”可以防止overfitting?一个所谓“显而易见”的解释就是:更小的权值w,从某种意义上说,表示网络的复杂度更低,对数据的拟合刚刚好(这个法则也叫做奥卡姆剃刀),而在实际应用中,也验证了这一点,L2正则化的效果往往好于未经正则化的效果。当然,对于很多人(包括我)来说,这个解释似乎不那么显而易见,所以这里添加一个稍微数学一点的解释(引自知乎):
过拟合的时候,拟合函数的系数往往非常大,为什么?如下图所示,过拟合,就是拟合函数需要顾忌每一个点,最终形成的拟合函数波动很大。在某些很小的区间里,函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值(绝对值)非常大,由于自变量值可大可小,所以只有系数足够大,才能保证导数值很大。
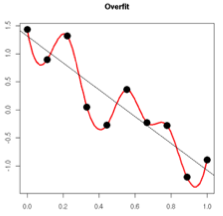
而正则化是通过约束参数的范数使其不要太大,所以可以在一定程度上减少过拟合情况。
4、Dropout
L1、L2正则化是通过修改代价函数来实现的,而Dropout则是通过修改神经网络本身来实现的,它是在训练网络时用的一种技巧(trike)。它的流程如下:
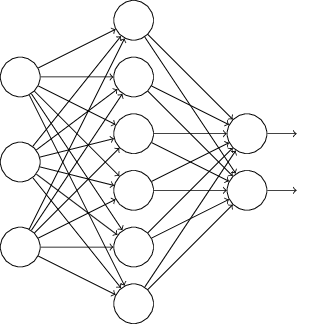
假设我们要训练上图这个网络,在训练开始时,我们随机地“删除”一半的隐层单元,视它们为不存在,得到如下的网络:

保持输入输出层不变,按照BP算法更新上图神经网络中的权值(虚线连接的单元不更新,因为它们被“临时删除”了)。
以上就是一次迭代的过程,在第二次迭代中,也用同样的方法,只不过这次删除的那一半隐层单元,跟上一次删除掉的肯定是不一样的,因为我们每一次迭代都是“随机”地去删掉一半。第三次、第四次……都是这样,直至训练结束。
以上就是Dropout,它为什么有助于防止过拟合呢?可以简单地这样解释,运用了dropout的训练过程,相当于训练了很多个只有半数隐层单元的神经网络(后面简称为“半数网络”),每一个这样的半数网络,都可以给出一个分类结果,这些结果有的是正确的,有的是错误的。随着训练的进行,大部分半数网络都可以给出正确的分类结果,那么少数的错误分类结果就不会对最终结果造成大的影响。

数据分析咨询请扫描二维码
若不方便扫码,搜微信号:CDAshujufenxi
以下的文章内容来源于刘静老师的专栏,如果您想阅读专栏《刘静:10大业务分析模型突破业务瓶颈》,点击下方链接 https://edu.cda ...
2025-04-23大咖简介: 刘凯,CDA大咖汇特邀讲师,DAMA中国分会理事,香港金管局特聘数据管理专家,拥有丰富的行业经验。本文将从数据要素 ...
2025-04-22CDA持证人简介 刘伟,美国 NAU 大学计算机信息技术硕士, CDA数据分析师三级持证人,现任职于江苏宝应农商银行数据治理岗。 学 ...
2025-04-21持证人简介:贺渲雯 ,CDA 数据分析师一级持证人,互联网行业数据分析师 今天我将为大家带来一个关于用户私域用户质量数据分析 ...
2025-04-18一、CDA持证人介绍 在数字化浪潮席卷商业领域的当下,数据分析已成为企业发展的关键驱动力。为助力大家深入了解数据分析在电商行 ...
2025-04-17CDA持证人简介:居瑜 ,CDA一级持证人,国企财务经理,13年财务管理运营经验,在数据分析实践方面积累了丰富的行业经验。 一、 ...
2025-04-16持证人简介: CDA持证人刘凌峰,CDA L1持证人,微软认证讲师(MCT)金山办公最有价值专家(KVP),工信部高级项目管理师,拥有 ...
2025-04-15持证人简介:CDA持证人黄葛英,ICF国际教练联盟认证教练,前字节跳动销售主管,拥有丰富的行业经验。在实际生活中,我们可能会 ...
2025-04-14在 Python 编程学习与实践中,Anaconda 是一款极为重要的工具。它作为一个开源的 Python 发行版本,集成了众多常用的科学计算库 ...
2025-04-14随着大数据时代的深入发展,数据运营成为企业不可或缺的岗位之一。这个职位的核心是通过收集、整理和分析数据,帮助企业做出科 ...
2025-04-11持证人简介:CDA持证人黄葛英,ICF国际教练联盟认证教练,前字节跳动销售主管,拥有丰富的行业经验。 本次分享我将以教培行业为 ...
2025-04-11近日《2025中国城市长租市场发展蓝皮书》(下称《蓝皮书》)正式发布。《蓝皮书》指出,当前我国城市住房正经历从“增量扩张”向 ...
2025-04-10在数字化时代的浪潮中,数据已经成为企业决策和运营的核心。每一位客户,每一次交易,都承载着丰富的信息和价值。 如何在海量客 ...
2025-04-09数据是数字化的基础。随着工业4.0的推进,企业生产运作过程中的在线数据变得更加丰富;而互联网、新零售等C端应用的丰富多彩,产 ...
2025-04-094月7日,美国关税政策对全球金融市场的冲击仍在肆虐,周一亚市早盘,美股股指、原油期货、加密货币、贵金属等资产齐齐重挫,市场 ...
2025-04-08背景 3月26日,科技圈迎来一则重磅消息,苹果公司宣布向浙江大学捐赠 3000 万元人民币,用于支持编程教育。 这一举措并非偶然, ...
2025-04-07在当今数据驱动的时代,数据分析能力备受青睐,数据分析能力频繁出现在岗位需求的描述中,不分岗位的任职要求中,会特意标出“熟 ...
2025-04-03在当今数字化时代,数据分析师的重要性与日俱增。但许多人在踏上这条职业道路时,往往充满疑惑: 如何成为一名数据分析师?成为 ...
2025-04-02最近我发现一个绝招,用DeepSeek AI处理Excel数据简直太爽了!处理速度嘎嘎快! 平常一整天的表格处理工作,现在只要三步就能搞 ...
2025-04-01你是否被统计学复杂的理论和晦涩的公式劝退过?别担心,“山有木兮:统计学极简入门(Python)” 将为你一一化解这些难题。课程 ...
2025-03-31