在文本挖掘中,主题模型是比较特殊的一块,它的思想不同于我们常用的机器学习算法,因此这里我们需要专门来总结文本主题模型的算法。本文关注于潜在语义索引算法(LSI)的原理。
1. 文本主题模型的问题特点
在数据分析中,我们经常会进行非监督学习的聚类算法,它可以对我们的特征数据进行非监督的聚类。而主题模型也是非监督的算法,目的是得到文本按照主题的概率分布。从这个方面来说,主题模型和普通的聚类算法非常的类似。但是两者其实还是有区别的。
聚类算法关注于从样本特征的相似度方面将数据聚类。比如通过数据样本之间的欧式距离,曼哈顿距离的大小聚类等。而主题模型,顾名思义,就是对文字中隐含主题的一种建模方法。比如从“人民的名义”和“达康书记”这两个词我们很容易发现对应的文本有很大的主题相关度,但是如果通过词特征来聚类的话则很难找出,因为聚类方法不能考虑到到隐含的主题这一块。
那么如何找到隐含的主题呢?这个一个大问题。常用的方法一般都是基于统计学的生成方法。即假设以一定的概率选择了一个主题,然后以一定的概率选择当前主题的词。最后这些词组成了我们当前的文本。所有词的统计概率分布可以从语料库获得,具体如何以“一定的概率选择”,这就是各种具体的主题模型算法的任务了。
当然还有一些不是基于统计的方法,比如我们下面讲到的LSI。
2. 潜在语义索引(LSI)概述
潜在语义索引(Latent Semantic Indexing,以下简称LSI),有的文章也叫Latent Semantic Analysis(LSA)。其实是一个东西,后面我们统称LSI,它是一种简单实用的主题模型。LSI是基于奇异值分解(SVD)的方法来得到文本的主题的。而SVD及其应用我们在前面的文章也多次讲到,比如:奇异值分解(SVD)原理与在降维中的应用和矩阵分解在协同过滤推荐算法中的应用。如果大家对SVD还不熟悉,建议复习奇异值分解(SVD)原理与在降维中的应用后再读下面的内容。
这里我们简要回顾下SVD:对于一个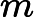
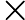
 m×n的矩阵
m×n的矩阵 A,可以分解为下面三个矩阵:
A,可以分解为下面三个矩阵:

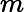
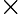
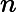

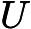
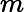
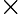
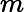
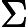
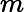
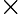
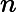
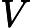
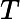
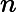
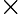
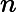 Am×n=Um×mΣm×nVn×nT
Am×n=Um×mΣm×nVn×nT
有时为了降低矩阵的维度到k,SVD的分解可以近似的写为:

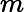
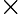
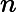

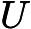
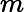
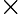
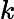
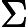
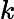
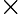
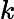
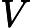
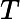
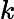
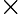
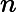 Am×n≈Um×kΣk×kVk×nT
Am×n≈Um×kΣk×kVk×nT
如果把上式用到我们的主题模型,则SVD可以这样解释:我们输入的有m个文本,每个文本有n个词。而
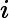
 Aij则对应第i个文本的第j个词的特征值,这里最常用的是基于预处理后的标准化TF-IDF值。k是我们假设的主题数,一般要比文本数少。SVD分解后,
Aij则对应第i个文本的第j个词的特征值,这里最常用的是基于预处理后的标准化TF-IDF值。k是我们假设的主题数,一般要比文本数少。SVD分解后,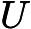
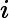
 Uil对应第i个文本和第l个主题的相关度。
Uil对应第i个文本和第l个主题的相关度。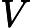

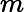 Vjm对应第j个词和第m个词义的相关度。
Vjm对应第j个词和第m个词义的相关度。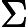

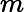 Σlm对应第l个主题和第m个词义的相关度。
Σlm对应第l个主题和第m个词义的相关度。
也可以反过来解释:我们输入的有m个词,对应n个文本。而
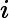
 Aij则对应第i个词档的第j个文本的特征值,这里最常用的是基于预处理后的标准化TF-IDF值。k是我们假设的主题数,一般要比文本数少。SVD分解后,
Aij则对应第i个词档的第j个文本的特征值,这里最常用的是基于预处理后的标准化TF-IDF值。k是我们假设的主题数,一般要比文本数少。SVD分解后,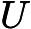
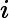
 Uil对应第i个词和第l个词义的相关度。
Uil对应第i个词和第l个词义的相关度。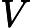

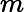 Vjm对应第j个文本和第m个主题的相关度。
Vjm对应第j个文本和第m个主题的相关度。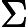

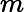 Σlm对应第l个词义和第m个主题的相关度。
Σlm对应第l个词义和第m个主题的相关度。
这样我们通过一次SVD,就可以得到文档和主题的相关度,词和词义的相关度以及词义和主题的相关度。
3. LSI简单实例
这里举一个简单的LSI实例,假设我们有下面这个有10个词三个文本的词频TF对应矩阵如下:
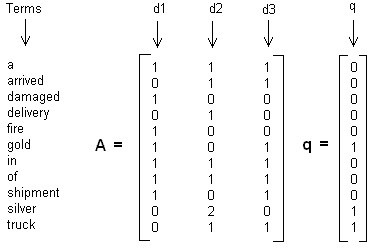
这里我们没有使用预处理,也没有使用TF-IDF,在实际应用中最好使用预处理后的TF-IDF值矩阵作为输入。
我们假定对应的主题数为2,则通过SVD降维后得到的三矩阵为:

从矩阵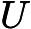
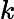 Uk我们可以看到词和词义之间的相关性。而从
Uk我们可以看到词和词义之间的相关性。而从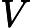
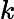 Vk可以看到3个文本和两个主题的相关性。大家可以看到里面有负数,所以这样得到的相关度比较难解释。
Vk可以看到3个文本和两个主题的相关性。大家可以看到里面有负数,所以这样得到的相关度比较难解释。
4. LSI用于文本相似度计算
在上面我们通过LSI得到的文本主题矩阵可以用于文本相似度计算。而计算方法一般是通过余弦相似度。比如对于上面的三文档两主题的例子。我们可以计算第一个文本和第二个文本的余弦相似度如下 :
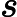

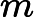
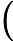
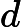


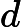













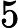
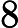







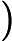
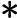
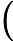







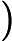
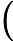






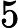
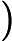
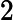







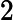

















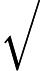
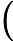





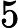
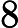
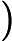
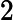

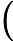







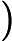
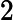




















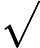 sim(d1,d2)=(−0.4945)∗(−0.6458)+(0.6492)∗(−0.7194)(−0.4945)2+0.64922(−0.6458)2+(−0.7194)2
sim(d1,d2)=(−0.4945)∗(−0.6458)+(0.6492)∗(−0.7194)(−0.4945)2+0.64922(−0.6458)2+(−0.7194)2
5. LSI主题模型总结
LSI是最早出现的主题模型了,它的算法原理很简单,一次奇异值分解就可以得到主题模型,同时解决词义的问题,非常漂亮。但是LSI有很多不足,导致它在当前实际的主题模型中已基本不再使用。
主要的问题有:
1) SVD计算非常的耗时,尤其是我们的文本处理,词和文本数都是非常大的,对于这样的高维度矩阵做奇异值分解是非常难的。
2) 主题值的选取对结果的影响非常大,很难选择合适的k值。
3) LSI得到的不是一个概率模型,缺乏统计基础,结果难以直观的解释。
对于问题1),主题模型非负矩阵分解(NMF)可以解决矩阵分解的速度问题。对于问题2),这是老大难了,大部分主题模型的主题的个数选取一般都是凭经验的,较新的层次狄利克雷过程(HDP)可以自动选择主题个数。对于问题3),牛人们整出了pLSI(也叫pLSA)和隐含狄利克雷分布(LDA)这类基于概率分布的主题模型来替代基于矩阵分解的主题模型。
回到LSI本身,对于一些规模较小的问题,如果想快速粗粒度的找出一些主题分布的关系,则LSI是比较好的一个选择,其他时候,如果你需要使用主题模型,推荐使用LDA和HDP。

数据分析咨询请扫描二维码
若不方便扫码,搜微信号:CDAshujufenxi
一、CDA持证人介绍 在数字化浪潮席卷商业领域的当下,数据分析已成为企业发展的关键驱动力。为助力大家深入了解数据分析在电商行 ...
2025-04-17CDA持证人简介:居瑜 ,CDA一级持证人,国企财务经理,13年财务管理运营经验,在数据分析实践方面积累了丰富的行业经验。 一、 ...
2025-04-16持证人简介: CDA持证人刘凌峰,CDA L1持证人,微软认证讲师(MCT)金山办公最有价值专家(KVP),工信部高级项目管理师,拥有 ...
2025-04-15持证人简介:CDA持证人黄葛英,ICF国际教练联盟认证教练,前字节跳动销售主管,拥有丰富的行业经验。在实际生活中,我们可能会 ...
2025-04-14在 Python 编程学习与实践中,Anaconda 是一款极为重要的工具。它作为一个开源的 Python 发行版本,集成了众多常用的科学计算库 ...
2025-04-14随着大数据时代的深入发展,数据运营成为企业不可或缺的岗位之一。这个职位的核心是通过收集、整理和分析数据,帮助企业做出科 ...
2025-04-11持证人简介:CDA持证人黄葛英,ICF国际教练联盟认证教练,前字节跳动销售主管,拥有丰富的行业经验。 本次分享我将以教培行业为 ...
2025-04-11近日《2025中国城市长租市场发展蓝皮书》(下称《蓝皮书》)正式发布。《蓝皮书》指出,当前我国城市住房正经历从“增量扩张”向 ...
2025-04-10在数字化时代的浪潮中,数据已经成为企业决策和运营的核心。每一位客户,每一次交易,都承载着丰富的信息和价值。 如何在海量客 ...
2025-04-09数据是数字化的基础。随着工业4.0的推进,企业生产运作过程中的在线数据变得更加丰富;而互联网、新零售等C端应用的丰富多彩,产 ...
2025-04-094月7日,美国关税政策对全球金融市场的冲击仍在肆虐,周一亚市早盘,美股股指、原油期货、加密货币、贵金属等资产齐齐重挫,市场 ...
2025-04-08背景 3月26日,科技圈迎来一则重磅消息,苹果公司宣布向浙江大学捐赠 3000 万元人民币,用于支持编程教育。 这一举措并非偶然, ...
2025-04-07在当今数据驱动的时代,数据分析能力备受青睐,数据分析能力频繁出现在岗位需求的描述中,不分岗位的任职要求中,会特意标出“熟 ...
2025-04-03在当今数字化时代,数据分析师的重要性与日俱增。但许多人在踏上这条职业道路时,往往充满疑惑: 如何成为一名数据分析师?成为 ...
2025-04-02最近我发现一个绝招,用DeepSeek AI处理Excel数据简直太爽了!处理速度嘎嘎快! 平常一整天的表格处理工作,现在只要三步就能搞 ...
2025-04-01你是否被统计学复杂的理论和晦涩的公式劝退过?别担心,“山有木兮:统计学极简入门(Python)” 将为你一一化解这些难题。课程 ...
2025-03-31在电商、零售、甚至内容付费业务中,你真的了解你的客户吗? 有些客户下了一两次单就消失了,有些人每个月都回购,有些人曾经是 ...
2025-03-31在数字化浪潮中,数据驱动决策已成为企业发展的核心竞争力,数据分析人才的需求持续飙升。世界经济论坛发布的《未来就业报告》, ...
2025-03-28你有没有遇到过这样的情况?流量进来了,转化率却不高,辛辛苦苦拉来的用户,最后大部分都悄无声息地离开了,这时候漏斗分析就非 ...
2025-03-27TensorFlow Datasets(TFDS)是一个用于下载、管理和预处理机器学习数据集的库。它提供了易于使用的API,允许用户从现有集合中 ...
2025-03-26