 京公网安备 11010802034615号
经营许可证编号:京B2-20210330
京公网安备 11010802034615号
经营许可证编号:京B2-20210330
前面的假设检验、方差分析基本上都是围绕差异性分析,不论是单个总体还是两个总体及以上,总之都是属于研究“区别”,从本节开始,我们关注“联系”,变量之间的关系分为 函数关系和相关关系。 本节这里重点探讨的是不同类型变量之间的相关性,千万记住一点相关性不代表因果性。除表中列出的常用方法外,还有Tetrachoric、相关系数等。
| 变量类型 | 变量类型 | 相关系数计算方法 | 示例 |
|---|---|---|---|
| 连续型变量 | 连续型变量 | Pearson(正态)/Spearman(非正态) | 商品曝光量和购买转化率 |
| 二分类变量(无序) | 连续型变量 | Point-biserial | 性别和疾病指数 |
| 无序分类变量 | 连续型变量 | 方差分析 | 不同教育水平的考试成绩 |
| 有序分类变量 | 连续型变量 | 连续指标离散化后当做有序分类 | 商品评分与购买转化率 |
| 二分类变量 | 二分类变量 | 数学公式: 检验 联合 Cramer's V | 性别和是否吸烟 |
| 二分类变量(有序) | 连续型变量 | Biserial | 乐器练习时间与考级是否通过 |
| 无序分类变量 | 无序分类变量 | 数学公式: 检验 / Fisher检验 | 手机品牌和年龄段 |
| 有序分类变量 | 无序分类变量 | 数学公式: 检验 | 满意度和手机品牌 |
| 有序分类变量 | 有序分类变量 | Spearman /Kendall Tau相关系数 | 用户等级和活跃程度等级 |
Pearson相关系数度量了两个连续变量之间的线性相关程度;
import random
import numpy as np
import pandas as pd
np.random.seed(10)
df = pd.DataFrame({'商品曝光量':[1233,1333,1330,1323,1323,1142,1231,1312,1233,1123],
'购买转化率':[0.033,0.034,0.035,0.033,0.034,0.029,0.032,0.034,0.033,0.031]})
df
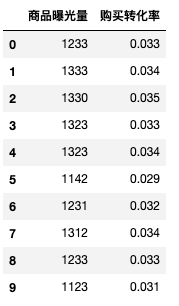
pd.Series.corr(df['商品曝光量'], df['购买转化率'],method = 'pearson') # pearson相关系数
# 0.885789300493948
import scipy.stats as stats
# 假设有两个变量X和Y
X = df['商品曝光量']
Y = df['购买转化率']
# 使用spearmanr函数计算斯皮尔曼相关系数和p值
corr, p_value = stats.pearsonr(X, Y)
print("Pearson相关系数:", corr)
print("p值:", p_value)
# Pearson相关系数: 0.8857893004939478
# p值: 0.0006471519603654732
Spearman等级相关系数可以衡量非线性关系变量间的相关系数,是一种非参数的统计方法,可以用于定序变量或不满足正态分布假设的等间隔数据;
import random
import numpy as np
import pandas as pd
np.random.seed(10)
df = pd.DataFrame({'品牌知名度排位':[9,4,3,6,5,8,1,7,10,2],
'售后服务质量评价排位':[8,2,5,4,7,9,1,6,10,3]})
df

pd.Series.corr(df['品牌知名度排位'], df['售后服务质量评价排位'],method = 'spearman') # spearman秩相关
# 0.8787878787878788
import scipy.stats as stats
# 假设有两个变量X和Y
X = df['品牌知名度排位']
Y = df['售后服务质量评价排位']
# 使用spearmanr函数计算斯皮尔曼相关系数和p值
corr, p_value = stats.spearmanr(X, Y)
print("斯皮尔曼相关系数:", corr)
print("p值:", p_value)
# 斯皮尔曼相关系数: 0.8787878787878788
# p值: 0.0008138621117322101
结论:p = 0.0008<0.05,表明两变量之间的正向关系很显著。
假设我们想要研究性别对于某种疾病是否存在影响。我们有一个二元变量“性别”(男、女)和一个连续型变量“疾病指数”。我们想要计算性别与疾病指数之间的相关系数,就需要用到Point-biserial相关系数。
import scipy.stats as stats
# 创建一个列表来存储数据
gender = [0, 1, 0, 1, 1, 0]
disease_index = [3.2, 4.5, 2.8, 4.0, 3.9, 3.1]
# 使用pointbiserialr函数计算Point-biserial相关系数和p值
corr, p_value = stats.pointbiserialr(gender, disease_index)
print("Point-biserial相关系数:", corr)
print("p值:", p_value)
# Point-biserial相关系数: 0.9278305692406299
# p值: 0.007624695507848026
结论:p = 0.007<0.05,表明两变量之间的正向关系很显著。即性别与疾病指数正相关
假设我们想要比较不同教育水平的学生在CDA考试成绩上是否存在显著差异。我们有一个无序分类变量“教育水平”(高中、本科、研究生)和一个连续型变量“考试成绩”。
import pandas as pd
import statsmodels.api as sm
from statsmodels.formula.api import ols
# 创建一个DataFrame来存储数据
data = pd.DataFrame({
'教育水平': ['高中', '本科', '本科', '研究生', '高中', '本科', '研究生'],
'考试成绩': [80, 90, 85, 95, 75, 88, 92]
})
# 使用ols函数创建一个线性模型
model = ols('考试成绩 ~ C(教育水平)', data=data).fit()
# 使用anova_lm函数进行方差分析
anova_table = sm.stats.anova_lm(model, typ=2)
anova_table

结论:p = 0.0102<0.05,拒绝原假设,表明两变量之间的正向关系很显著。教育水平与考试成绩正相关
将连续型变量离散化后当做有序分类,然后用 有序分类变量 VS 有序分类变量的方法
一项研究调查了不同性别的成年人对在公众场合吸烟的态度,结果如表所示。那么,性别与对待吸烟的态度之间的相关程度
| - | 赞同 | 反对 |
|---|---|---|
| 男 | 15 | 10 |
| 女 | 10 | 26 |
import numpy as np
from scipy.stats import chi2_contingency
observed = np.array([[15, 10],
[10, 26]])
observed
chi2, p, dof, expected = chi2_contingency(observed,correction =False) # correction =False
# 卡方值
# P值
# 自由度:
# 与原数据数组同维度的对应期望值
chi2, p
#(6.3334567901234555, 0.011848116168529757)
结论:p = 0.0118<0.05,拒绝原假设,表明两变量之间的正向关系很显著。
phi = np.sqrt(chi2/n)
print("phi's V:", phi)
# phi's V: 0.3222222222222222
这里只列出 指标 和 Cramer V指标 的计算,其他计算方式请读者自行研究。
# 计算Cramer's V
contingency_table = observed
n = contingency_table.sum().sum()
phi_corr = np.sqrt(chi2 / (n * min(contingency_table.shape) - 1))
v = phi_corr / np.sqrt(min(contingency_table.shape) - 1)
print("Cramer's V:", v)
# Cramer's V: 0.22878509151645754
import numpy as np
from scipy.stats import pearsonr
# 生成随机的二元变量
binary_variable = np.random.choice([0, 1], size=100)
# 生成随机的连续变量
continuous_variable = np.random.normal(loc=0, scale=1, size=100)
# 注:此处的代码未经严格考证,请谨慎使用
def biserial_correlation(binary_variable, continuous_variable):
binary_variable_bool = binary_variable.astype(bool)
binary_mean = np.mean(binary_variable_bool)
binary_std = np.std(binary_variable_bool)
binary_variable_norm = (binary_variable_bool - binary_mean) / binary_std
corr, _ = pearsonr(binary_variable_norm, continuous_variable)
biserial_corr = corr * (np.std(continuous_variable) / binary_std)
return biserial_corr
# 计算Biserial相关系数
biserial_corr = biserial_correlation(binary_variable, continuous_variable)
print("Biserial相关系数:", biserial_corr)
Biserial相关系数: -0.2061772328681707
参考 检验
参考 检验
Kendall秩相关系数也是一种非参数的等级相关度量,类似于Spearman等级相关系数。
import random
import numpy as np
import pandas as pd
np.random.seed(10)
df = pd.DataFrame({'品牌知名度排位':[9,4,3,6,5,8,1,7,10,2],
'售后服务质量评价排位':[8,2,5,4,7,9,1,6,10,3]})
df
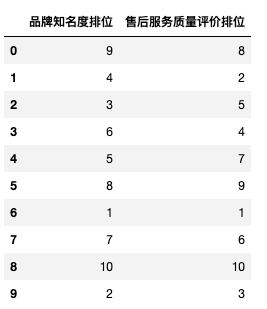
pd.Series.corr(df['品牌知名度排位'], df['售后服务质量评价排位'],method = 'kendall') # Kendall Tau相关系数
# 0.7333333333333333
from scipy.stats import kendalltau
# 两个样本数据
x = df['品牌知名度排位']
y = df['售后服务质量评价排位']
# 计算Kendall Tau相关系数
correlation, p_value = kendalltau(x, y)
print("Kendall Tau相关系数:", correlation)
print("p值:", p_value)
# Kendall Tau相关系数: 0.7333333333333333
# p值: 0.002212852733686067
浮生皆纵,恍如一梦,让我们只争朝夕,不负韶华!
下期将为大家带来《统计学极简入门》之 再看t检验、F检验、检验
《CDA一级教材》适合CDA一级考生备考,也适合业务及数据分析岗位的从业者提升自我。完整电子版已上线CDA网校,累计已有10万+在读~

免费加入阅读:https://edu.cda.cn/goods/show/3151?targetId=5147&preview=0

数据分析咨询请扫描二维码
若不方便扫码,搜微信号:CDAshujufenxi
在零售行业从“流量争夺”转向“价值深耕”的演进中,塔吉特百货(Target)以两场标志性实践树立了行业标杆——2000年后的孕妇精 ...
2025-12-15在统计学领域,二项分布与卡方检验是两个高频出现的概念,二者都常用于处理离散数据,因此常被初学者混淆。但本质上,二项分布是 ...
2025-12-15在CDA(Certified Data Analyst)数据分析师的工作链路中,“标签加工”是连接原始数据与业务应用的关键环节。企业积累的用户行 ...
2025-12-15在Python开发中,HTTP请求是与外部服务交互的核心场景——调用第三方API、对接微服务、爬取数据等都离不开它。虽然requests库已 ...
2025-12-12在数据驱动决策中,“数据波动大不大”是高频问题——零售店长关心日销售额是否稳定,工厂管理者关注产品尺寸偏差是否可控,基金 ...
2025-12-12在CDA(Certified Data Analyst)数据分析师的能力矩阵中,数据查询语言(SQL)是贯穿工作全流程的“核心工具”。无论是从数据库 ...
2025-12-12很多小伙伴都在问CDA考试的问题,以下是结合 2025 年最新政策与行业动态更新的 CDA 数据分析师认证考试 Q&A,覆盖考试内容、报考 ...
2025-12-11在Excel数据可视化中,柱形图因直观展示数据差异的优势被广泛使用,而背景色设置绝非简单的“换颜色”——合理的背景色能突出核 ...
2025-12-11在科研实验、商业分析或医学研究中,我们常需要判断“两组数据的差异是真实存在,还是偶然波动”——比如“新降压药的效果是否优 ...
2025-12-11在CDA(Certified Data Analyst)数据分析师的工作体系中,数据库就像“数据仓库的核心骨架”——所有业务数据的存储、组织与提 ...
2025-12-11在神经网络模型搭建中,“最后一层是否添加激活函数”是新手常困惑的关键问题——有人照搬中间层的ReLU激活,导致回归任务输出异 ...
2025-12-05在机器学习落地过程中,“模型准确率高但不可解释”“面对数据噪声就失效”是两大核心痛点——金融风控模型若无法解释决策依据, ...
2025-12-05在CDA(Certified Data Analyst)数据分析师的能力模型中,“指标计算”是基础技能,而“指标体系搭建”则是区分新手与资深分析 ...
2025-12-05在回归分析的结果解读中,R方(决定系数)是衡量模型拟合效果的核心指标——它代表因变量的变异中能被自变量解释的比例,取值通 ...
2025-12-04在城市规划、物流配送、文旅分析等场景中,经纬度热力图是解读空间数据的核心工具——它能将零散的GPS坐标(如外卖订单地址、景 ...
2025-12-04在CDA(Certified Data Analyst)数据分析师的指标体系中,“通用指标”与“场景指标”并非相互割裂的两个部分,而是支撑业务分 ...
2025-12-04每到“双十一”,电商平台的销售额会迎来爆发式增长;每逢冬季,北方的天然气消耗量会显著上升;每月的10号左右,工资发放会带动 ...
2025-12-03随着数字化转型的深入,企业面临的数据量呈指数级增长——电商的用户行为日志、物联网的传感器数据、社交平台的图文视频等,这些 ...
2025-12-03在CDA(Certified Data Analyst)数据分析师的工作体系中,“指标”是贯穿始终的核心载体——从“销售额环比增长15%”的业务结论 ...
2025-12-03在神经网络训练中,损失函数的数值变化常被视为模型训练效果的“核心仪表盘”——初学者盯着屏幕上不断下降的损失值满心欢喜,却 ...
2025-12-02